GOFAI
Efter sommaren på Dartmouth 1956 föddes AI-fältet med målet: att återskapa mänskligt tänkande i en maskin. Den dominerande filosofin på, ofta kallad Symbolisk AI eller GOFAI (Good Old-Fashioned Artificial Intelligence), byggde på idén att intelligens inte var en mystisk biologisk process, utan en formell, logisk manipulation av symboler. Målet var att bygga tänkande från grunden med logikens och matematikens verktyg.
Denna vision gav upphov till två huvudsakliga, parallella angreppssätt föratt skapa intelligens:
-
Kunskap och logiskt resonemang: Detta läger fokuserade på att fånga vad en expert vet. Genom att bygga en formell kunskapsbas med fakta och regler, och sedan använda en slutledningsmotor för att dra logiska slutsatser, var målet att bygga en "tänkare" – ett system som kunde resonera, diagnostisera och förklara.
-
Problemlösning och sökning: Det andra lägret såg intelligens som förmågan att planera och agera. Här definierades problem som att hitta en väg från ett starttillstånd till ett önskat måltillstånd. Genom att utveckla strategier för att systematiskt söka igenom ett hav av möjligheter, var målet att bygga en "görare" – ett system som kunde navigera, lösa pussel och planera sekvenser av handlingar.
Det här kapitlet utforskar båda dessa angreppssätt. Vi kommer att se deras teoretiska grunder, deras praktiska framgångar i allt från medicinska expertsystem till spel-AI, och hur de till slut stötte på samma fundamentala hinder – en "den kombinatoriska explosionen" – som ledde till de vad vi kallar AI-vintrar och banade väg för en annorlunda syn på artificiell intelligens. Praktiska exempel på expertsystem täcks i slutet av boken i djupdykningarna.
Det är värt att nämna att fler strategier och underdomäner av symbolisk AI existerar, men här täcker vi några av de huvudsakliga koncepten. Några fler exempel täcks i djupdykningarna.
En sista poäng om symbolisk AI är att dessa strategier kunde användas för att skapa system som kunde lösa väldigt kognitivt utmanande problem, och kunde således uppfattas som intelligenta vid den här tiden. Nu är dessa strategier sånt som programmerare, oavsett om de planerar att arbeta inom AI, förväntas lära sig idag. Den deterministiska naturen av dessa strategier gör att vi idag sällan tänker på dessa strategier som AI.
Personligen skulle jag hellre kalla det clever use of programming and mathematics.
Notera att de inte är omöjligt att den frasen förblir aktuell även i kommande inriktningar av AI som vi skall utforska.
Kunskap och logiskt resonemang
För att skapa en tänkare behövdes två saker: ett sätt att representera kunskap och en "motor" för att resonera kring den kunskapen.
Innan en AI kan "tänka" måste den veta något om världen. Processen att omvandla mänsklig kunskap till ett format en dator kan förstå kallas kunskapsrepresentation. Inom symbolisk AI gör man detta med två typer av byggstenar: fakta och regler.
Faktabas
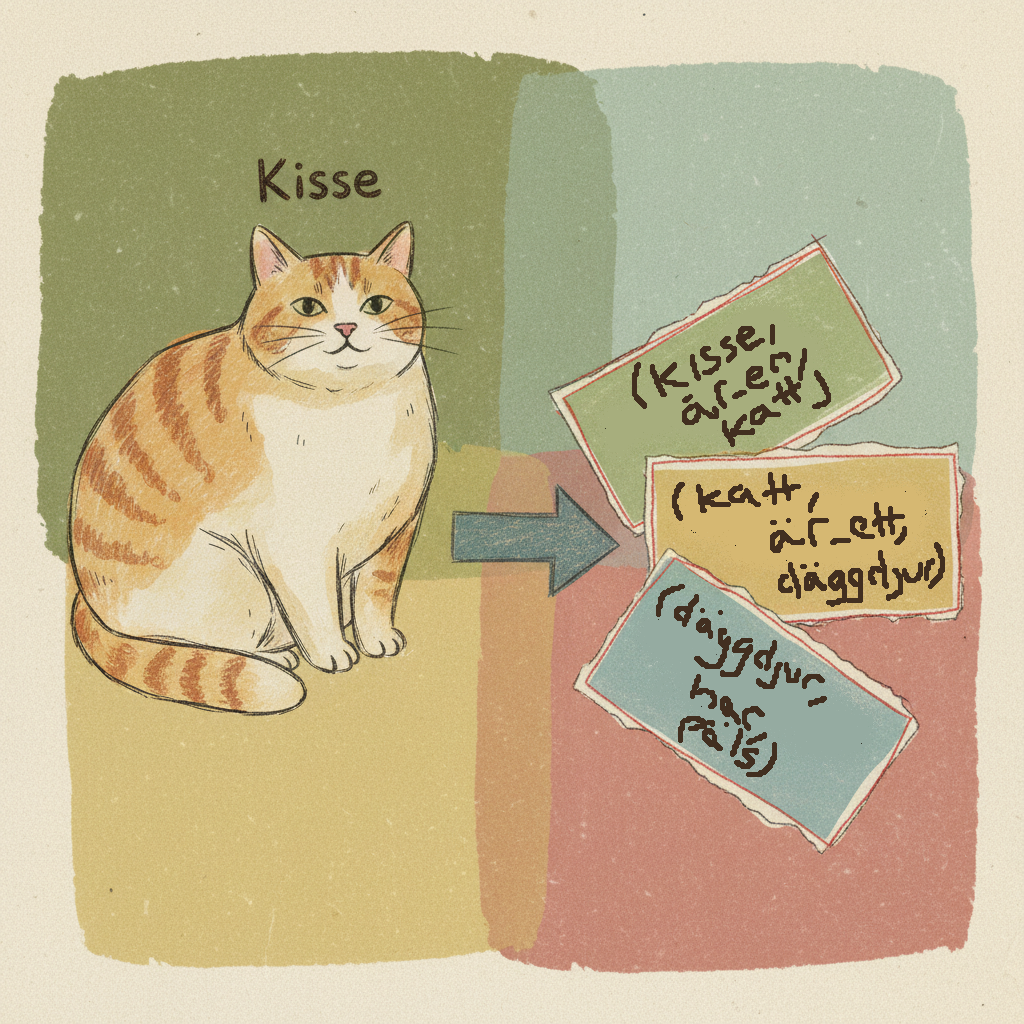
Först skapar man en faktabas (Knowledge Base). Tänk dig den som en låda med digitala faktablad, där varje blad är ett enkelt, tydligt påstående. Ofta skrivs dessa som en trippel: (subjekt, relation, objekt).
(Kisse, är_en, Katt)(Katt, är_ett, Däggdjur)(Däggdjur, har, Päls)
Orden Kisse, Katt, Däggdjur och Päls är symboler. De är etiketter datorn använder för att representera koncept och ting. Här är en symbol är bara en textsträng som representerar något.
Regelbas
En låda full med fakta är inte smart. Den kan bara lagra information. Den verkliga "intelligensen" uppstår när man lägger till en regelbas (Rule Base) – en uppsättning instruktioner för hur man kan kombinera och skapa nya fakta. Dessa kallas ofta produktionsregler och har en enkel OM-DÅ (IF-THEN) struktur.
En sådan regel skulle kunna vara:
OM (?x, är_en, ?y) OCH (?y, är_ett, ?z), DÅ (?x, är_ett, ?z).
Här är ?x, ?y och ?z variabler – platshållare som kan matcha vilka symboler som helst. Regeln är en generell mall för logiskt resonemang (exemplet är en transitiv relation).
System som bygger på denna OM-DÅ-logik kallas regelbaserade system. Nu kan AI:n, eller mer specifikt dess slutledningsmotor (Inference Engine), börja arbeta. Motorn testar systematiskt reglerna mot faktabasen för att dra nya slutsatser.
Slutledningsmetoder
Slutledningsmotorn kan arbeta på två huvudsakliga sätt för att dra olika slutsatser, dessa presenteras nedan.
Forward Chaining
Denna metod utgår från kända fakta och ser vart de leder. Den är datastyrt. Man matar in data i ena änden och låter logikens kedjereaktion arbeta sig framåt för att se vilken slutsats som dyker upp.
Hur det fungerar (förenklat):
- Start: Titta på alla fakta i faktabasen.
- Matcha: Gå igenom alla regler. Finns det någon regel vars
OM-del matchar de kända fakta?- Ja! Regeln
OM (?x, är_en, ?y) OCH (?y, är_ett, ?z)matchar fakta(Kisse, är_en, Katt)och(Katt, är_ett, Däggdjur). Här blir?x = Kisse,?y = Katt,?z = Däggdjur.
- Ja! Regeln
- Agera: Skapa den nya slutsatsen från regelns
DÅ-del:(Kisse, är_ett, Däggdjur). - Upprepa: Lägg till den nya faktan i faktabasen och börja om från steg 1. Processen fortsätter tills inga nya fakta kan skapas.
Detta är som en detektiv som samlar alla ledtrådar på ett bord och sedan systematiskt ser vilka slutsatser som kan dras.
Backward Chaining
Denna metod fungerar tvärtom. Istället för att utgå från fakta, börjar den med ett mål eller en hypotes och arbetar sig baklänges för att se om den kan bevisas. Den är målstyrd.
Hur det fungerar (förenklat):
- Mål: Kan vi bevisa påståendet
(Kisse, har, Päls)? - Sök regel: Finns det någon regel som kan skapa denna slutsats i sin
DÅ-del?- Ja! Låt oss säga att vi har regeln:
OM (?x, är_ett, Däggdjur), DÅ (?x, har, Päls).
- Ja! Låt oss säga att vi har regeln:
- Nytt delmål: För att bevisa vårt mål måste vi nu bevisa regelns
OM-del:(Kisse, är_ett, Däggdjur). Detta blir vårt nya mål. - Upprepa: Systemet startar om från steg 1 med det nya målet.
- Mål: Kan vi bevisa
(Kisse, är_ett, Däggdjur)? - Sök regel: Ja, vår transitivitetsregel från förut kan skapa detta.
- Nya delmål: För att bevisa detta måste vi bevisa
(Kisse, är_en, ?y)OCH(?y, är_ett, Däggdjur).
- Mål: Kan vi bevisa
- Sök fakta: Systemet letar nu i faktabasen.
- Den hittar
(Kisse, är_en, Katt).?yblirKatt. - Den kollar delmål 2:
(Katt, är_ett, Däggdjur). Det finns också i faktabasen!
- Den hittar
- Bevisat: Alla delmål är bevisade. Hela kedjan är komplett. Den ursprungliga hypotesen
(Kisse, har, Päls)är sann.
Detta är som en advokat som har ett mål ("min klient är oskyldig") och arbetar baklänges för att hitta de bevis och argument som stödjer det.
Idén bakom symbolisk AI är både enkel och kraftfull: Om vi kan bryta ner komplexa resonemang till tillräckligt många enkla, logiska steg (symboler och regler), kan vi återskapa intelligens i en maskin. Det är ett försök att bygga tänkande från grunden, som att bygga ett hus med logikens legobitar.
Expertsystem
nder 70- och 80-talen fann symbolisk AI sin första stora kommersiella tillämpning i form av Expertsystem. Idén var att fånga en mänsklig experts kunskap inom ett mycket snävt område (t.ex. medicinsk diagnos, geologisk prospektering) och koda in den som en serie OM-DÅ-regler. Detta skapade en "AI-boom" och ledde till att företag som Symbolics och Lisp Machines växte fram och lockade till sig stora investeringar.
För ett komplext problem som medicinsk diagnos var Forward Chaining ineffektivt. Det vore som att lista en patients alla symptom och sedan blint testa alla tusentals möjliga sjukdomar. En riktig läkare jobbar inte så; hen använder sin erfarenhet för att snabbt fokusera på de mest sannolika diagnoserna.
Därför använde de mest framgångsrika expertsystemen, som det berömda MYCIN för blodinfektioner, den smartare strategin Backward Chaining. Genom att börja med en hypotes (ett mål) och arbeta sig baklänges, undvek systemet att slösa tid på osannolika vägar. MYCINs "tankeprocess" kunde se ut så här:
- MÅL (Hypotes): Kan patienten ha bakterieinfektionen streptococcus?
- KONTROLLERA REGEL: Min regelbok säger att för att bevisa streptococcus, måste jag veta om
(A) patienten har feberOCH(B) blodprovet visar X. - NYTT DELMÅL: Försök bevisa
(A). Systemet letar i sin faktabas. Om faktan inte finns, ställer den en fråga till användaren: "Har patienten feber?" - UPPREPA: Om svaret är ja, går den vidare till delmål
(B). Om svaret är nej, överges hypotesen om streptococcus och systemet testar nästa möjliga sjukdom.
Denna målstyrda metod var mycket effektivare. I tester presterade MYCIN faktiskt bättre på att ställa rätt diagnos än många nyexaminerade läkare. Experter hade konsulteras för att avgöra i vilken ordning som hypoteserna skulle behandlas. Det var alltså programmerarens uppdrag att manuellt försöka fånga och representera kunskapen i systemet.
Problemlösning och sökning
Parallellt med försöken att koda kunskap, insåg forskare att en annan form av intelligens låg i att kunna planera och agera. Istället för att fråga 'Vad är sant?', frågade man 'Vad ska jag göra härnäst?'. Detta ledde till idén om problemlösning som en systematisk sökning.
En sökalgoritm är ett smart sätt för datorn att ta reda på hur man går från ett startläge till ett mål , t.ex. att hitta den bästa vägen i en labyrint eller spelet Pac-Man! Sökalgoritmer är grunden för intelligent beteende i datorprogram. De gör det möjligt för en dator att:
- Ta beslut
- Lösa problem steg för steg
- Navigera i komplexa miljöer
- Hitta optimal eller tillräckligt bra lösning utan att prova allt
Formalisera sökproblem
Grundtanken är att omvandla ett problem till en formell struktur som en algoritm kan förstå. Tänk dig att du ska hitta snabbaste vägen från Malmö till Stockholm med bil. Detta kan formaliseras som följande sökproblem:
- Tillståndsrum (State Space): Alla möjliga städer du kan befinna dig i (Malmö, Lund, Jönköping, Linköping, Stockholm, etc.).
- Starttillstånd (Initial State): Du är i Malmö.
- Måltillstånd (Goal State): Du vill nå Stockholm.
- Operatorer (Operators): De handlingar som tar dig mellan tillstånd, dvs. att köra en viss väg mellan två städer.
- Kostnad (Cost): Varje operator har en kostnad, t.ex. avståndet i kilometer eller tiden i minuter.
- Lösning (Solution): En sekvens av städer (en väg) från start till mål, t.ex.
Malmö -> Jönköping -> Linköping -> Stockholm. En optimal lösning är den väg som har den lägsta totala kostnaden.
Detta ramverk är otroligt flexibelt och kan appliceras på allt från att lösa ett Sudoku (där varje tillstånd är en delvis ifylld bräda) till att planera en robots rörelser.
Den kombinatoriska explosionen
Varför är detta svårt? För att antalet möjliga vägar i ett problem kan bli astronomiskt stort. Om du från varje stad kan köra till 5 andra städer, och du måste passera minst 10 städer för att komma fram, har du redan 5^10 (nästan 10 miljoner) möjliga vägar att utvärdera. Detta kallas den kombinatoriska explosionen. Att blint testa varje enskild väg är oftast omöjligt inom en rimlig tidsram.
Här kommer sökalgoritmerna in. De är strategier för att smart navigera detta enorma "sökträd" av möjligheter utan att nödvändigtvis behöva undersöka allt.
Vi säger att en sökalgoritm är komplett om den är garanterad att hitta en lösning på problemet ifall det finns en. Vi säger också att den är optimal om den är garanterad att hitta den kortaste eller på annat sätt mest optimala lösningen (lägst kostnad / lägst antal operationer osv, beror på sölproblemet).
Oinformerad sökning (Blind Search)
Dessa algoritmer har ingen extra information om problemet. De känner inte till avståndet till målet och utforskar systematiskt sökträdet baserat på en enkel strategi.
Depth-First Search (DFS) - Djupet först
DFS är en oinformerad sökalgoritm som fungerar genom att gå så djupt som möjligt i en gren av sökträdet, innan den backar tillbaka och testar en annan väg. Tänk dig att du ska hitta vägen genom en labyrint: DFS skulle välja en riktning och gå tills det inte går längre, och först då vända om och prova nästa väg.
- Datastruktur: Använder en Stack (en LIFO, Last-In-First-Out-struktur). En stack fungerar som en stapel med tallrikar: det sista du lägger in är det första som tas ut. I DFS betyder det att vi alltid utforskar den senaste vägen först, vilket gör att vi kommer så djupt som möjligt innan vi backar.
- Egenskaper:
- Minnes-effektiv: Behöver bara lagra den nuvarande vägen.
- Inte optimal: Hittar inte nödvändigtvis den kortaste vägen. Den kan ta en lång omväg och hitta en lösning, helt omedveten om att en mycket kortare väg fanns nära starten.
- Inte komplett: Kan gå vilse i oändliga loopar om den inte håller reda på vilka tillstånd den redan besökt.
Exempel: DFS i en enkel graf
Låt oss se hur DFS fungerar med en konkret graf med 5 noder. Vi börjar från nod 0.
- Start: Besök nod 0. Lägg dess grannar (1 och 3) i stacken. Stack:
[3, 1] - Steg 1: Ta översta noden från stacken: nod 1. Besök den. Lägg dess obesökta granne (2) i stacken. Stack:
[3, 2] - Steg 2: Ta översta noden: nod 2. Besök den. Lägg dess obesökta granne (4) i stacken. Stack:
[3, 4] - Steg 3: Ta översta noden: nod 4. Besök den. Den har inga nya grannar. Stack:
[3] - Steg 4: Ta översta noden: nod 3. Besök den. Den har inga nya grannar. Stack:
[] - Klar: Stacken är tom.
Besöksordningen blev: 0 → 1 → 2 → 4 → 3.
Breadth-First Search (BFS) - Bredden först
BFS är den försiktiga, metodiska strategin. Den utforskar alla närliggande tillstånd först, i expanderande "ringar" från startpunkten.
- Datastruktur: Använder en Kö (en FIFO, First-In-First-Out-struktur). Som en vanlig kö i en affär: den som kommer först blir betjänad först. BFS utforskar alltså vägar i den ordning de upptäcktes.
- Egenskaper:
- Optimal: Garanterar att hitta den kortaste vägen (om alla steg har samma kostnad).
- Komplett: Kommer garanterat att hitta en lösning om en finns.
- Minnes-krävande: Måste lagra alla upptäckta vägar i minnet, vilket kan bli enormt för stora problem.
Informerad sökning (Heuristic Search)
De blinda sökalgoritmerna är systematiska men naiva. De stöter snabbt på problemet med den kombinatoriska explosionen: för varje litet extra steg i ett problem (som ett drag i schack) ökar antalet framtida möjligheter exponentiellt. Att undersöka varenda väg är ohållbart.
Det var uppenbart att mänsklig intelligens inte fungerade så. En schackmästare ser inte alla möjliga drag; hon ser de bra dragen. Detta var insikten som ledde till ett av symbolisk AI:s centrala koncept: heuristiken.
En heuristik är en smart genväg, en tumregel eller en strategi som hjälper till att lösa ett problem utan att garantera en perfekt lösning. Det är en metod för att göra en kvalificerad gissning och beskära det gigantiska sökträdet till en hanterbar storlek. I kontexten av sökalgoritmer ger vi algoritmen en "magkänsla" för hur lovande en väg är.
Denna magkänsla formaliseras i en heuristikfunktion, ofta kallad h(n), som är en tillåten (admissible) gissning av kostnaden från ett givet tillstånd n till målet. "Tillåten" betyder att den aldrig får överskatta den verkliga kostnaden. Den måste vara optimistisk. I vårt vägexempel skulle en bra heuristik vara fågelvägen från en stad till Stockholm, eftersom den verkliga bilresan aldrig kan vara kortare än så.
A* Search (A-stjärna)
A* är den mest kända och använda informerade sökalgoritmen. Den kombinerar det bästa från två världar:
- Den känner till den exakta kostnaden från start till det nuvarande tillståndet,
g(n). - Den använder heuristiken
h(n)för att gissa kostnaden som återstår.
Den prioriterar att utforska den nod som har det lägsta värdet på f(n) = g(n) + h(n).
A* väljer alltså den väg som ser ut att vara den totalt sett kortaste. Genom att balansera redan avlagd sträcka med en optimistisk gissning om framtiden kan A* på ett otroligt effektivt sätt undvika att utforska dåliga vägar och fokusera på de som är mest lovande. Om heuristiken är tillåten, garanterar A* att hitta den optimala lösningen, mycket snabbare än BFS.
Detta är en central och viktig fråga. Kravet på att heuristiken aldrig får överskatta den verkliga kostnaden är det som garanterar att A* hittar den absolut bästa lösningen. Man kan sammanfatta logiken med två principer:
-
"Håll dörren öppen"-principen: A* kommer aldrig att definitivt överge en outforskad väg så länge dess potentiella bästa kostnad (det optimistiska löftet
f(n)) är lägre än den bästa verkliga lösningen den redan hittat. Den måste överväga alla vägar som *kan vara* kortare. -
"Släng och glöm"-principen: Omvänt, om till och med den mest optimistiska gissningen för en väg (
f(n)) är sämre än en lösning du redan har, kan den vägen tryggt ignoreras för alltid. Den verkliga kostnaden kan omöjligt bli bättre än sin egen optimistiska gissning.
En superoptimistisk gissning kan få A* att *tillfälligt* utforska en sämre väg, men den verkliga kostnaden (g(n)) kommer snabbt att väga upp för den dåliga gissningen. Algoritmen kommer då att inse sitt misstag och byta till en mer lovande väg. Denna säkerhetsmekanism garanterar att den till slut landar på den optimala lösningen.
Avslutning
Trots sina olika angreppssätt – att bygga en "tänkare" eller en "görare" – stötte båda pelarna av symbolisk AI till slut på samma fundamentala hinder: verkligheten.
Micro-worlds
Forskarna insåg snabbt att det var oerhört svårt att skapa regler för hela den stökiga, oförutsägbara verkligheten. Lösningen blev att skapa så kallade "Micro-worlds" – små, avgränsade, virtuella världar med en egen, perfekt logik.
Ett berömt exemplet var SHRDLU, utvecklat av Terry Winograd vid MIT i slutet av 60-talet. SHRDLU var ett program som lät en användare konversera med en robotarm i en virtuell värld fylld med olikfärgade klossar, pyramider och lådor. Användaren kunde skriva kommandon på naturligt språk, som "Plocka upp den stora röda klossen" eller "Hitta en kloss som är högre än den du håller i och ställ den i lådan".

SHRDLU kunde förstå tvetydiga kommandon, ställa klargörande frågor och till och med "minnas" vad den hade gjort tidigare. För en kort tid såg det ut som att problemet med språkförståelse var på väg att lösas.
Men SHRDLUs framgång var också dess största svaghet: den fungerade bara i sin egen, extremt begränsade värld. Så fort man ställde en fråga om något utanför klossarna, som "Vad är meningen med livet?" eller "Är du hungrig?", bröt illusionen samman.
SHRDLU visade att det är relativt enkelt att skapa en AI som verkar intelligent inom en extremt begränsad och väldefinierad domän. Problemet, som forskarna smärtsamt skulle upptäcka, är att dessa system är "bräckliga" (brittle). De går sönder så fort de stöter på något som inte finns i deras regelbok. Verkligheten är inte en prydlig mikrovärld.
Detta visade på två grundläggande problem som drabbade hela den symboliska AI-eran:
-
Bräcklighet & brist på sunt förnuft: Både expertsystemen och sökalgoritmerna var "bräckliga" (brittle). De fungerade bara så länge världen betedde sig exakt enligt deras inprogrammerade karta eller regelbok. De saknade helt sunt förnuft – den intuitiva, kroppsliga förståelsen av världen som människor använder för att hantera oväntade situationer. Filosofen Hubert Dreyfus var den skarpaste kritikern och menade att mänsklig expertis är en intuitiv, mönstermatchande förmåga (System 1) som inte kan kokas ner till formella regler (System 2).
-
Kunskapsinhämtningens flaskhals: All kunskap var tvungen att kodas in manuellt. Det var en enorm manuell ansträngning att antingen intervjuua en expert och skriva tusentals regler för ett expertsystem, eller att designa en effektiv heuristikfunktion för en komplex sökalgoritm. Att skala upp var praktiskt taget omöjligt.
AI-vintrar
Hypen kring AI varade inte. När de grundläggande problemen visade sig vara för svåra att lösa med de strategier som använts, sprack bubblan. Ouppnådda förväntnignar ledde till två perioder av strypt finansiering, kända som "AI-vintrar":
-
Den första AI-vintern (mitten av 70-talet): Utlöstes av två förödande rapporter.
- I Storbritannien dömde Lighthill-rapporten (1973) ut AI-forskningen för att ha misslyckats med att hantera den kombinatoriska explosionen. Även boken What Computers Can't Do (1972) av Herbert Dreyfus målar upp en liknande bild av att AI-forskare överdrivit eller missuppskattat grovt hur långt utvecklingen kunde nå under 60-70talet.
- I USA publicerades ALPAC-rapporten (1966), som konstaterade att maskinöversättning (t.ex. ryska till engelska) var dyrare och sämre än mänskliga översättare. Detta ströp finansieringen för språkteknologi i över ett decennium.
- Samtidigt pågick en inbördes konflikt inom AI mellan "The Neats" (som ville ha ren, matematisk logik) och "The Scruffies" (som trodde på röriga, ad-hoc lösningar som "bara funkade"). Denna splittring försvagade fältets trovärdighet.
-
Den andra AI-vintern (sent 80-tal/tidigt 90-tal): Orsakades av att de kommersiella expertsystemen inte kunde leva upp till sina löften. De var för dyra, för bräckliga och för svåra att underhålla.
Det är värt att nämna att den symboliska AI:n inte var ensamt ansvarig, men andra samtida alternativa inriktningar på hur man kan skapa AI hade också vid denna tid misslyckas leverera i den utsträckning som kunde upplevas som utlovat.
Perspektiv på den symboliska AI:n
Biologiskt & evolutionärt
Symbolisk AI är ett försök att bygga intelligens som man bygger ett hus efter en färdig ritning ("top-down"). AI-vintern visade att denna metod är bräcklig. Naturens metod, evolutionen, är istället en "bottom-up"-process. Den har ingen ritning, utan använder trial-and-error i massiv skala för att "odla" fram komplexa system som anpassar sig till en stökig värld.
Ekonomiskt
80-talets boom och fall för expertsystemen är ett skolboksexempel på en Gartner Hype Cycle: en teknisk trigger leder till uppblåsta förväntningar, en investeringsbubbla, en krasch av desillusion, och slutligen en långsam, mer mogen återhämtning.
Psykologiskt
Redan 1966 visade chatboten ELIZA hur djupt rotad vår tendens är att projera förståelse och känslor på ett system, även om vi vet att det är en simpel illusion. Denna ELIZA-effekt avslöjar mer om vår mänskliga psykologi än om tekniken, och den har blivit en central del av affärsmodellen för dagens AI-assistenter och kompanjoner.
- ELIZA (1966): En enkel chatbot som simulerade en psykoterapeut genom att vända användarens meningar till frågor.
- Användare: "Jag är ledsen över min mamma."
- ELIZA: "Berätta mer om din mamma."
- Effekten: Människor, även de som visste hur den fungerade, reagerade känslomässigt och projicerade förståelse på programmet.
- ELIZA-effekten: Vår djupt rotade tendens att tillskriva mänskliga egenskaper (känslor, intention) till datorsystem.
Kulturellt
Robotarna C-3PO och R2-D2 från Star Wars är perfekta exempel på symbolisk AI: högst specialiserade expertsystem för protokoll och astromekanik. De är briljanta inom sina snäva domäner men saknar flexibilitet och sunt förnuft. ED-209 från Robocop är den mörka sidan – ett regelsystem som är så bräckligt att det leder till katastrof eftersom det inte kan hantera kontext som avviker från dess programmering.
Misslyckandet med den symboliska AI:n visade att intelligens kanske inte kunde designas som en perfekt ritning. Forskare började ställa en ny, radikal fråga: Tänk om vi inte behöver programmera reglerna alls? Tänk om maskinen kan lära sig dem själv, bara genom att titta på världen? Detta var startskottet för en ny revolution: Maskininlärning.
Övningar
Övning 2 : Sökalgoritmer
För att öva på de fyra täckta sökalgoritmerna ska du få styra Pac-Man som navigerar genom olika labyrinter, genom att implementera dessa algoritmena.
Följ dessa steg
1. Öppna GitHub
2. Klona repot till din dator:
Öppna din terminal (CMD, PowerShell eller terminal i VS Code) och skriv följande:
pip install future
Om ovan misslyckades får du gå tillbaka till början av boken där vi täckte installation av python. Se till att du klickar i när du installerar python att python skall läggas till i PATH på datorn.
git clone https://github.com/majabeskow/berkeley_pacman.git
cd berkeley_pacman
code .
4. Kör en sökning med en redan given sökalgoritm:
python pacman.py --layout tiny_maze -p SearchAgent -a fn=tiny_maze_search
Om du inte kan köra programmet, se över att du står i rätt mapp /berkeley_pacman och att python är installerat som det ska, samt biblioteket future.
5. Hitta filen search.py
- Hitta funktionen depth_first_search i search.py
- Det är här vi kommer att skriva vår DFS-algoritm
- Läs igenom tiny_maze_search implementationen som du precis körde.
- Notera att en implementation returnerar en lista av rörelser.
- Dessa rörelser är dem som tar pacman från start till mål.
- Läs även igenom Koden för SearchProblem
- SearchProblem är klassen som skickas in som argument till sökfunktionen du skall skriva.
- Du kommer använda en del av dessa metoder för att t.ex. hitta vägar, startpunkt och avgöra om en punkt är slutpunkten.
- Det finns en "example_maze_search" som endast visar hur man kan interagera med "SearchProblem" klassen.
Testa kör example_maze_search också:
python pacman.py --layout tiny_maze -p SearchAgent -a fn=example_maze_search
Implementera DFS
Här är en modifierad pseudokod för DFS.
Olika datastrukturer används för att hålla koll på olika saker.
För att kunna returnera en lista av rörelser kan vi:
- När vi upptäcker en nod, spara från vilken nod den upptäcktes.
- När vi upptäcker en nod, spara vilken rörelse(action) som tar pacman till den noden
När vi hittar målet kan vi skapa listan av rörelser genom att gå baklänges från målet och kolla för varje nod vilken rörelse som togs, och från vilken nod, hela vägen till starten, och sedan returnera dessa rörelser i en lista.
def depth_first_search(problem: SearchProblem) -> list(Directions):
# Du behöver en datastruktur för att hålla koll på upptäckta noder som du inte än har besökt
# Du kan använda en Stack som finns i util.py
# När du gör stack.push(node) läggs en nod till längst upp på stacken
# När du gör node = stack.pop() plockar du ut den senaste tillagda noden
stack = TODO # skapa en util.Stack()
# Du behöver en datastruktur för att hålla koll på redan upptäckta noder
# så att du inte lägger till samma nod flera gånger. Du kan använda lista eller set.
# lista ut hur man gör en lista i python
# ... hehehe
discovered = TODO # skapa en lista
# För att hålla koll på vilken väg din sökning tog behöver du alltså spara undan
# för varje nod, vem som upptäckte den och vilken rörelse som rör roboten från
# "upptäckare" till "den upptäckta"
# En map, key-value store, eller dictionary som det heter i python är bra
# Då kan "nyckeln" vara den "upptäckta noden", och för varje "upptäckt nod"
# kan värdet vi sparar vara "upptäckaren" och "rörelsen"
# Två värden kan slås ihop till en variabel med hjälp av en tupel.
# t.ex.
# discovered_path["b"] = ("a","north")
# indikerar att vår dictionary, discovered_path (som också skulle kunna kallas parents)
# har sparat informationen att för att nå noden "b" så kan vår robot gå "north" från "a"
discovered_path = TODO # skapa en dictionary
# lägg till startnoden till stacken
# klassen problem har en funktion för att hämta startnoden.
start = problem.TODO
stack.push(TODO)
# lägg till startnoden till de upptäckta noderna
discovered.TODO
# indikera att det inte finns någon nod som används för att ta oss till startnoden
discovered_path[TODO] = (
None,
None,
) # startnoden har alltså ingen (upptäckare,rörelse) tupel
while stack is not empty: # TODO kolla i util.py vilka funktioner stack har.
node = TODO # hämta ut senaste tillagda noden på stacken (SÅ FUNGERAR DFS!)
# utforska grannar om vi inte nått målet
if node is not goal:
# för varje hittad granne, hitta:
# namnet på grannen, rörelsen för att ta sig dit, kostnaden att ta sig dit
# Kolla på klassen SearchProblem.
# Vad heter funktionen för att hitta alla grannar till en nod?
for neighbor, action, cost in problem.TODO(node):
if neighbor not in discovered:
# lägg till grannen som upptäckt
discovered.TODO
# lägg till vilken nod som upptäckte grannen, och via vilken rörelse
discovered_path[neighbor] = (node, action)
# lägg till grannen på stacken
stack.TODO
else: # målet funnet!!
# Dags att hämta alla åtgärder för att nå målet!
path = TODO # ny tom lista
current = (
node # variabeln current håller koll på vilken nod vi "backat" till
)
# backa hela vägen till starten
while current is not start:
# för varje nod, hämta vilken nod den upptäcktes ifrån och via vilken rörelse
parent_node, action = discovered_path[current]
# lägg till "rörelsen" längst fram i den "path" du skapar
path.TODO(action)
# backa till föregående nod
current = parent_node
# När loopen är över har vi backat hela vägen till starten och kan ge en korrekt "path"
return path
# Sökningen är över utan att en nod upptäckts som är slutnoden
raise Exception("Failed to find a solution")
När du är klar och vill testa din kod :
python pacman.py --layout tiny_maze -p SearchAgent -a fn=dfs
Mål: Pac-Man ska kunna ta sig till målet med hjälp av just din DFS!
Breadth-First Search (BFS)
Fortsätt med BFS. Till skillnad från DFS, som du implementerade i föregående övning, garanterar BFS att du hittar den kortaste vägen till maten.
Uppgift: Implementera BFS i search.py
- Hitta din kod: Öppna filen
search.pyi din Pac-Man-projektmapp. - Implementera
breadth_first_search: Hitta funktionenbreadth_first_searchoch fyll i den. Du kommer att behöva använda en Kö (Queue) frånutil.py.
Tips:
- Kön i
util.pyharpush(item)ochpop()metoder. - Du behöver hålla koll på besökta noder för att undvika cykler.
- Vi använder samma parent dict som i DFS för att rekonstruera vägen.
Pseudocode for BFS (memory-efficient):
def breadth_first_search(problem: SearchProblem) -> list(Directions):
# BFS använder en kö (Queue) för att hålla koll på upptäckta noder som vi inte än har besökt.
# Detta är den stora skillnaden mot DFS!
# En kö fungerar enligt "först in, först ut"-principen.
# När du gör queue.push(node) läggs en nod till sist i kön.
# När du gör node = queue.pop() plockar du ut den nod som lades till först.
queue = TODO # skapa en util.Queue()
# Precis som i DFS behöver vi hålla koll på redan upptäckta noder
# så att vi inte hamnar i en oändlig loop om det finns cykler i grafen.
#
#
discovered = TODO # skapa en lista eller ett set
# Vi behöver också spara vägen. En dictionary är perfekt för detta,
# där nyckeln är en nod och värdet är en tupel med (föregående_nod, åtgärd).
# t.ex. discovered_path["b"] = ("a", "north")
discovered_path = TODO # skapa en dictionary
# Börja med att lägga till startnoden i kön och markera den som upptäckt.
start_node = problem.TODO
queue.push(start_node)
discovered.append(start_node) # Lägg till i listan över upptäckta
# Startnoden har ingen föregångare.
discovered_path[start_node] = (None, None)
# Sökningen fortsätter så länge det finns noder kvar att besöka i kön.
while not queue.is_empty():
# Hämta ut den första noden som lades till i kön (SÅ FUNGERAR BFS!)
node = queue.pop()
# Har vi nått målet?
if problem.is_goal_state(node):
# Målet är funnet! Dags att återskapa vägen.
path = [] # Skapa en tom lista för vår väg
current = node
# Backa från målnoden till startnoden med hjälp av vår dictionary.
while current != start_node:
parent_node, action = discovered_path[current]
# Lägg till varje åtgärd i början av listan för att få rätt ordning.
path.insert(0, action)
current = parent_node
return path # Returnera den färdiga vägen
# Om vi inte nått målet, utforska grannarna.
# problem.getSuccessors(node) ger oss en lista med (granne, åtgärd, kostnad).
for neighbor, action, cost in problem.get_successors(node):
if neighbor not in discovered:
# Om vi hittar en ny, oupptäckt granne:
# 1. Markera den som upptäckt.
discovered.append(neighbor)
# 2. Spara hur vi kom hit (från vilken nod och med vilken åtgärd).
discovered_path[neighbor] = (node, action)
# 3. Lägg till den sist i kön för att besöka den senare.
queue.push(neighbor)
# Sökningen är över utan att en nod upptäckts som är slutnoden
raise Exception("Failed to find a solution")
Kör din BFS-agent
När du har implementerat din algoritm kan du testa den på medium_maze.
python pacman.py -l medium_maze -p SearchAgent -a fn=bfs
Reflektion
- Kör både DFS och BFS på
medium_maze. Vilken algoritm hittar den kortaste vägen? Varför? - Titta på antalet "Nodes expanded" som skrivs ut i terminalen. Vilken algoritm utforskar flest noder för att hitta lösningen i
medium_maze? Vad säger det om deras effektivitet?
Uniform Cost Search (UCS)
Uniform Cost Search (UCS) är en sökalgoritm som hittar den billigaste vägen från en startnod till en målnod i en viktad graf. Till skillnad från BFS, som hittar den kortaste vägen i termer av antal kanter (en väg mellan två noder kallas kant), hittar UCS vägen med den lägsta totala kostnaden.
Uppgift: Implementera UCS i search.py
- Hitta din kod: Öppna filen
search.py. - Implementera
uniform_cost_search: Hitta funktionenuniform_cost_searchoch fyll i den. Du kommer att behöva använda en Prioritetskö (PriorityQueue) frånutil.py.
Tips:
- Prioritet: I UCS är
prioritetenalltid den totala kostnaden (g(n)) för en väg från start till en nod. - (Viktigt!):
- Du kommer ofta att hitta en väg till en nod (t.ex. G) som inte är den kortaste. Låt oss säga att den har kostnad 10. Du lägger till den i prioritetskön.
- Algoritmen fortsätter att utforska andra, billigare vägar först. Senare hittar den en bättre väg till G med kostnad 6 och lägger även till denna i kön.
- Garantin: Prioritetskön kommer alltid att returnera vägen med kostnad 6 först. När du "processar" den och lägger G i din
besökta-mängd, har du låst in den bästa vägen. - När den dyrare vägen med kostnad 10 så småningom tas ut ur kön, kommer din kod att se att G redan är besökt och helt enkelt ignorera den.
- Slutsats: Det är möjligt att hitta en dyrare väg först, men det är omöjligt att processa den före den billigare vägen. Detta är varför algoritmen alltid hittar den bästa lösningen.
- "Lazy" initialisering: Klassiska beskrivningar av Dijkstra's initierar alla noder med oändlig kostnad. Vår implementation är "lazy" – vi lägger bara till noder i kön när vi hittar dem. Detta är mycket mer effektivt för stora problem som Pac-Man där vi inte känner till hela kartan från början.
Pseudocode for UCS (memory-efficient):
def breadth_first_search(problem: SearchProblem) -> list(Directions):
# BFS använder en kö (Queue) för att hålla koll på upptäckta noder som vi inte än har besökt.
# Detta är den stora skillnaden mot DFS!
# En kö fungerar enligt "först in, först ut"-principen.
# När du gör queue.push(node) läggs en nod till sist i kön.
# När du gör node = queue.pop() plockar du ut den nod som lades till först.
queue = TODO # skapa en util.Queue()
# Precis som i DFS behöver vi hålla koll på redan upptäckta noder
# så att vi inte hamnar i en oändlig loop om det finns cykler i grafen.
#
#
discovered = TODO # skapa en lista eller ett set
# Vi behöver också spara vägen. En dictionary är perfekt för detta,
# där nyckeln är en nod och värdet är en tupel med (föregående_nod, åtgärd).
# t.ex. discovered_path["b"] = ("a", "north")
discovered_path = TODO # skapa en dictionary
# Börja med att lägga till startnoden i kön och markera den som upptäckt.
start_node = problem.TODO
queue.push(start_node)
discovered.append(start_node) # Lägg till i listan över upptäckta
# Startnoden har ingen föregångare.
discovered_path[start_node] = (None, None)
# Sökningen fortsätter så länge det finns noder kvar att besöka i kön.
while not queue.is_empty():
# Hämta ut den första noden som lades till i kön (SÅ FUNGERAR BFS!)
node = queue.pop()
# Har vi nått målet?
if problem.is_goal_state(node):
# Målet är funnet! Dags att återskapa vägen.
path = [] # Skapa en tom lista för vår väg
current = node
# Backa från målnoden till startnoden med hjälp av vår dictionary.
while current != start_node:
parent_node, action = discovered_path[current]
# Lägg till varje åtgärd i början av listan för att få rätt ordning.
path.insert(0, action)
current = parent_node
return path # Returnera den färdiga vägen
# Om vi inte nått målet, utforska grannarna.
# problem.getSuccessors(node) ger oss en lista med (granne, åtgärd, kostnad).
for neighbor, action, cost in problem.get_successors(node):
if neighbor not in discovered:
# Om vi hittar en ny, oupptäckt granne:
# 1. Markera den som upptäckt.
discovered.append(neighbor)
# 2. Spara hur vi kom hit (från vilken nod och med vilken åtgärd).
discovered_path[neighbor] = (node, action)
# 3. Lägg till den sist i kön för att besöka den senare.
queue.push(neighbor)
# Sökningen är över utan att en nod upptäckts som är slutnoden
raise Exception("Failed to find a solution")
Kör din UCS-agent
När du har implementerat din algoritmin kan du testa den på medium_maze med 2 olika sökagenter som har olika kostnader för operationer beroende på hur långt västerut/österut operationerna är.
python pacman.py --layout medium_maze -p StayWestSearchAgent
python pacman.py --layout medium_maze -p StayEastSearchAgent
Reflektion
- UCS vs. Dijkstra's algoritm: Vad är skillnaden? I praktiken, för att hitta en väg till ett enda mål, är de identiska. Konceptuellt sett används Dijkstra's oftast för att beskriva algoritmen som hittar den kortaste vägen från en startnod till alla andra noder, medan UCS fokuserar på att hitta den kortaste vägen till ett specifikt mål. UCS är alltså Dijkstra's anpassad för ett söktillämpning.
A* Search
A* (A-star) är en kraftfull sökalgoritm som kombinerar kostnaden för vägen hittills med en heuristisk uppskattning av kostnaden som återstår. Detta gör den mycket effektivare än blinda sökalgoritmer som BFS.
Uppgift: Implementera A* i search.py
- Hitta din kod: Öppna filen
search.py. - Implementera
a_star_search: Hitta funktionena_star_searchoch fyll i den. Du kommer att behöva använda en Prioritetskö (PriorityQueue) frånutil.py.
Tips:
- A* är i grunden samma algoritm som UCS. Den enda skillnaden är hur prioriteten i kön beräknas.
- I stället för att bara använda den ackumulerade kostnaden
g(n)som prioritet, lägger A* till en heuristisk uppskattningh(n). - Prioriteten blir
f(n) = g(n) + h(n), därg(n)är den verkliga kostnaden att nå noden n ochh(n)är den optimistiskt uppskattade kostnaden som återstår till målet.
Pseudocode for A* (memory-efficient):
def a_star_search(problem : SearchProblem, heuristic=heuristics.your_heuristic) -> list(Directions):
# A* använder också en prioritetskö, precis som UCS.
# Skillnaden är hur vi beräknar prioriteten för varje nod.
# sökningen använder en funktion som argument (ovan "heuristic")
# Den används som följer h_value = heuristic(node,problem)
priority_queue = TODO # skapa en util.PriorityQueue()
# Vi behöver en dictionary för att spara den hittills billigaste kostnaden från start (g-värdet).
# Detta är identiskt med `cost_to_reach` i UCS.
# t.ex. g_cost["c"] = 12
g_cost = TODO # skapa en dictionary
# Precis som tidigare sparar vi vägen för att kunna återskapa den på slutet.
discovered_path = TODO # skapa en dictionary
# Vi behöver också hålla koll på noder vi redan har besökt,
# för att inte göra dubbelarbete, på samma sätt som i UCS
visited = TODO # skapa en lista eller ett set
# Allt börjar vid startnoden.
start_node = problem.get_start_state()
# Startnoden har ingen "upptäckare".
discovered_path[start_node] = (None, None)
# Vad är kostnaden (g-värdet) att nå startnoden från sig själv?
g_cost[start_node] = TODO
# Här kommer den stora skillnaden mot UCS!
# Vi måste också beräkna den uppskattade kostnaden från start till mål (h-värdet).
# Funktionen `heuristic` tar en nod och problemet som input.
h_value = heuristic(TODO, problem)
# A*s prioritet är f-värdet = g-värdet + h-värdet.
f_value = g_cost[start_node] + h_value
# Lägg till startnoden i kön med dess f-värde som prioritet.
priority_queue.push(TODO, TODO)
while not priority_queue.is_empty():
# Hämta ut noden med lägst f-värde (bäst kombination av redan rest och uppskattat kvar).
node = priority_queue.pop()
# Om vi redan har besökt denna nod, hoppa över den.
if node in visited:
continue
# Lägg till noden i listan över besökta noder.
visited.add(node)
# Om vi poppar målet har vi hittat den optimala lösningen (om heuristiken är "tillåten").
if problem.is_goal_state(node):
# Återskapa vägen precis som i de andra algoritmerna.
path = [] # ny tom lista
current = node
# backa hela vägen till starten
while current != start_node:
# för varje nod, hämta vilken nod den upptäcktes ifrån och via vilken rörelse
parent_node, action = discovered_path[current]
# lägg till "rörelsen" längst fram i den "path" du skapar
path.insert(0, action)
# backa till föregående nod
current = parent_node
# När loopen är över har vi backat hela vägen till starten och kan ge en korrekt "path"
return path
# Utforska grannar.
# Vad heter funktionen för att hitta alla grannar till en nod?
for neighbor, action, step_cost in problem.TODO(node):
# Beräkna grannens nya g-värde (kostnad från start) om vi går via den nuvarande noden.
new_g_cost = g_cost[TODO] + step_cost
# Om vi inte sett denna granne förut, ELLER om vi hittat en ny, billigare väg dit:
if neighbor not in g_cost or new_g_cost < g_cost[neighbor]:
# 1. Spara (eller uppdatera) det nya, lägre g-värdet.
g_cost[neighbor] = new_g_cost
# 2. Spara (eller uppdatera) vägen som ledde hit.
discovered_path[neighbor] = (TODO, TODO)
# 3. Beräkna det nya f-värdet för grannen.
new_h_value = heuristic(TODO, problem)
new_f_value = TODO # f(n) = g(n) + h(n)
# 4. Lägg till grannen i kön med dess nya f-värde som prioritet.
priority_queue.push(TODO, TODO)
# Sökningen är över utan att en nod upptäckts som är slutnoden
raise Exception("Failed to find a solution")
Kör din A*-agent
A*-funktionen tar emot en heuristic-funktion som argument. Pac-Man-projektet tillhandahåller manhattan_heuristic.
python pacman.py -l big_maze -p SearchAgent -a fn=astar,heuristic=manhattan_heuristic
Reflektion
- Jämför prestandan (antal expanderade noder) för BFS och A* på
big_maze. Varför är A* så mycket effektivare? - Heuristiken är en "gissning". Vad skulle hända om din heuristik var väldigt dålig och alltid returnerade 0? Vilken algoritm skulle A* då bete sig som?
- Detta kan du testa med
null_heuristic
- Detta kan du testa med
Övning 3: Den Oskrivbara Regelboken - Hur man korsar en gata
Syfte: Att på ett extremt konkret sätt illustrera Hubert Dreyfus poäng om att mänsklig expertis och "sunt förnuft" inte kan fångas i regler, varken på papper eller i kod.
Del 1: Skapa Regelboken
- Gruppuppgift: Försök att skriva en komplett regelbok (en serie
OM-DÅ-regler) som en robot skulle behöva följa för att säkert korsa en trafikerad gata. Var så detaljerade som möjligt.
Del 2: Hitta Luckorna (Diskussion)
- Diskutera era regler. Leta efter luckor, undantag och tvetydigheter.
- "Vad händer OM det regnar och sikten är dålig?"
- "Vad händer OM en bil blinkar höger men fortsätter rakt fram?"
- "Vad händer OM du får ögonkontakt med en förare som vinkar åt dig att gå?"
- "Hur kodifierar man regeln 'se självsäker ut så att bilarna stannar'?"
- "Vad händer om en lös hund springer ut på gatan?"
Ni kommer snabbt att upptäcka att antalet regler blir oändligt (den kombinatoriska explosionen) och att många regler är beroende av en intuitiv, social förståelse som är nästan omöjlig att skriva ner.
Reflektion: Hur är denna övning en perfekt illustration av bräcklighetsproblemet (brittleness) och sunt förnuft-problemet (common sense problem) som diskuteras i texten?
Övning 4: Spel-AI Arkeologi
Syfte: Att analysera och "reverse-engineera" den enkla, regelbaserade AI:n i klassiska videospel.
Instruktioner:
- Titta på videoklipp av NPC-beteenden (Non-Player Character) från äldre spel. Exempel:
- Goombas i Super Mario Bros. (går framåt, vänder vid ett hinder eller en kant).
- Vakter i det första Metal Gear (patrullerar i ett fast mönster, reagerar bara på det som är i deras exakta synfält).
- Fiender i Space Invaders (rör sig i en synkroniserad formation, flyttar sig ett steg ner när de når kanten).
- Uppgift: Försök i grupper att skriva ner den exakta, enkla uppsättningen
OM-DÅ-regler som styr karaktärens beteende. - Diskutera: Varför var dessa enkla regler tillräckliga på den tiden? Hur har erfarna spelare lärt sig att utnyttja (exploit) denna förutsägbarhet? Vad säger det om bräckligheten i regelbaserade system?
Källmaterial
- Hubert Dreyfus: Läs dessa få utvalda delar från What Computers Can't Do (1972). Den extra intresserade kan läsa uppföljaren What Computers Still Can't Do (1992) för att se hur hans argument utvecklades.
- Läs Introduction (xv)
- Läs The Future of Artificial Intelligence (203) och avsluta efter att du tittat på tabellen på nästa sida (204).
- Läs The Biological assumption (71) som kriticerar optimismen kring möjligheten av att modellera ett datorprogram likt hur den mänskliga hjärnan är strukturerad.
- Lighthill-rapporten & Debatten: Läs en sammanfattning av Lighthill-rapporten (1973) och se sedan klipp från den efterföljande TV-debatten "The Lighthill Debate" (BBC, 1973) där AI-pionjärer som Donald Michie och John McCarthy försvarar sitt fält.
Reflektionsfrågor
- Dreyfus: Dreyfus argumenterade för att mänsklig expertis är kroppslig och intuitiv. Efter att ha försökt skriva en regelbok för att korsa en gata, i vilken utsträckning håller ni med? Ge exempel från era egna liv på expertkunskap (från sport, musik, hantverk, social interaktion etc.) som ni tror är omöjlig att helt formalisera i regler.
- Lighthill: I debatten efter rapporten var stämningen minst sagt laddad. Varför tror ni att kritiken i Lighthill-rapporten väckte så starka känslor? Ser ni några paralleller till hur dagens AI-forskare och kritiker debatterar med varandra? Tror ni att en liknande "vinter" skulle kunna hända igen med dagens AI-hype?
Syfte: Att koppla det historiska ELIZA-experimentet till moderna AI-interaktioner och utforska de psykologiska och etiska dimensionerna.
Instruktioner:
- Interagera med ELIZA: Testa en online-version av ELIZA (sök på "ELIZA chatbot"). Notera hur den fungerar och hur det känns att prata med den.
- Diskutera i grupper:
- Även om ni vet att ELIZA bara är ett enkelt program, kände ni någon gång en tendens att tolka dess svar som förstående eller empatiska?
- Var kan vi se "ELIZA-effekten" idag? (Tänk på chatbots för kundtjänst, digitala assistenter som Siri/Alexa, eller AI-kompanjoner som Replika).
- Filmen Her (2013) utforskar en romantisk relation mellan en människa och ett AI-operativsystem. Är detta en oundviklig framtid, eller en varnande berättelse?
- Joseph Weizenbaum, ELIZAs skapare, blev en av sina egna skapelses största kritiker. Han var förskräckt över hur snabbt människor anförtrodde sig åt ett program han visste var en "parodi". Varför tror ni att han reagerade så starkt? Håller ni med om hans oro?
- Är det etiskt försvarbart av företag att designa AI-system som medvetet utnyttjar ELIZA-effekten för att skapa känslomässiga band med användare? Var går gränsen mellan ett hjälpsamt verktyg och känslomässig manipulation?