Machine Learning

Den symboliska AI:n gav oss en stor uppsättning fantastiska verktyg som är relevanta än idag. Men förhoppningar om att nästa stora genombrott inom AI skulle komma från den inriktningen är sedan länge borta.

När intresset för den symboliska AI:n avtog fanns det istället utrymme för en annan idé att växa fram. En idé som faktiskt föddes innan termen "Artificiell Intelligens" ens fanns. Det var idén om att inte programmera intelligens, utan att träna den. Att inte bygga logik, utan att bygga en hjärna som kan lära sig.

Connectionism

Redan 1943, långt innan AI-fältet fick sitt namn, hade Warren McCulloch och Walter Pitts skapat en matematisk modell av en biologisk neuron. 1958 byggde Frank Rosenblatt Perceptronen, en maskin som kunde lära sig känna igen former. New York Times skrev att detta var embryot till en dator som kommer att kunna gå, prata, se, skriva, reproducera sig själv och vara medveten om sin existens.¹

1969 publicerades dock boken Perceptrons av Marvin Minsky och Seymour Papert. I den bevisade de matematiskt att dessa tidiga nätverk hade fundamentala begränsningar (som vi ska se). Finansieringen ströps, forskarna bytte spår, och connectionismen fick klicka på snooze-knappen i bakgrunden i årtionden, medan den symboliska AI:n tog över scenen.

Men när expertsystemen misslyckades, började forskare damma av de gamla idéerna igen. De insåg att felet inte låg i idén om neuroner, utan i att vi hade haft för få av dem och för lite data.

Neuronen

Nervceller, som också kallas neuroner är en del av nervsystemet vars uppgift är att via signaler styra och koordinera kroppens olika funktioner. Vi behöver dem för att kunna reagera på information som skickas från våra sinnen och reagera på dem. Vi behöver dem för att kunna tänka och minnas saker. Över 80 miljarder neuroner uppskattas finnas i en mänsklig hjärna.

Översiktligt består nervcellen av en cellkropp och två olika typer av utskott som är högst relevanta för oss: dendriter, som tar emot signaler, och en axon, som skickar vidare signaler. Slutet av axonen förgrenar sig i flera axonterminaler så att signalen kan skickas vidare i massa olika riktningar.

Synapser kallas den struktur som bildas mellan neuroners axoner och andra neuroners dendriter. Synapsen överför signalerna som kommer via axonen, nervtråden, till receptorer på dendriten. Signalen som kommer via axonen är elektrisk och kan antingen skickas vidare som en elektrisk impuls eller omvandlas till en kemisk signal och skickas via neurotransmittorer.

När flera neuroner är sammankopplade kallar vi dem tillsammans ett neuralt nätverk.

En avgörande egenskap är vår hjärnas plasticitet, dess förmåga att skapa nya förbindelser eller på annat sätt ändra sin struktur och funktion. Detta sker som svar på yttre och inre påverkningar och tillåter oss att lära oss nya saker, kompensera för skador, anpassa oss till nya förutsättningar och bilda minner.

Connectionism representerar idén om att vi kanske kan skapa artificiell intelligens genom att bygga system som behandlar och överför information på liknande sätt. Med små sammankopplade, ofta simpla enheter, som tillsammans bildar något oerhört kapabelt.

Den artificiella neuronen

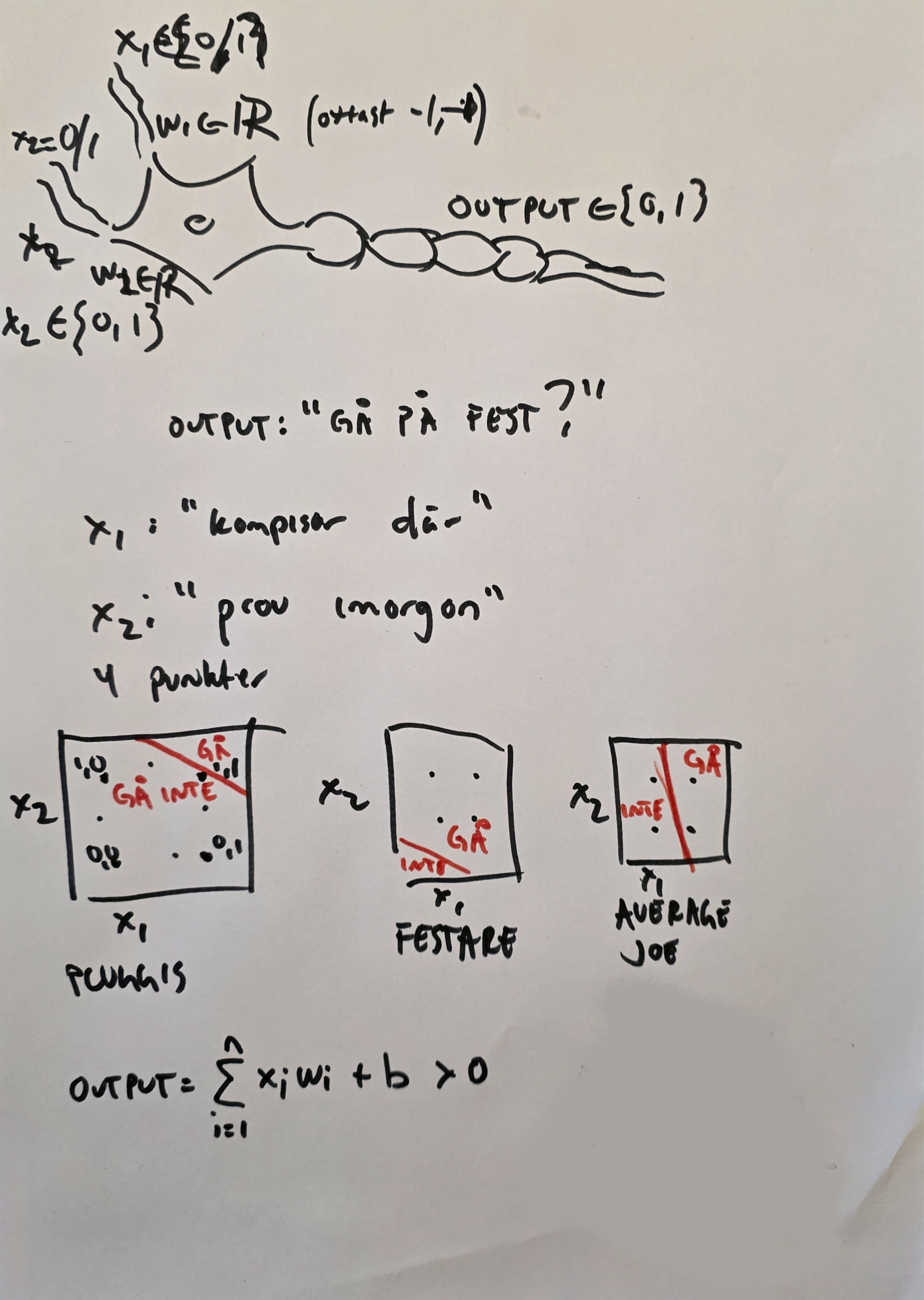
Tänk dig en neuron som en enkel beslutsmodell. Dess jobb är att väga samman olika informationskällor (inputs) för att fatta ett ja/nej-beslut (output). Låt oss använda en konkret, tvådimensionell analogi: Ska jag gå på festen?

För att fatta detta beslut har du två grundläggande frågor:

x1: Är vänner där? (1 för Ja, 0 för Nej)
x2: Har jag ett prov imorgon? (1 för Ja, 0 för Nej)

Denna artificiella neuronmodell representerar resonemanget med två justerbara "rattar" för varje fråga, kallade vikter (w1, w2), samt en tredje, oberoende ratt kallad bias (b).

Vikterna representerar hur viktig varje faktor är. En hög positiv vikt för w1 betyder "det är superviktigt att mina vänner är där". En stor negativ vikt för w2 betyder "ett prov är en stark anledning att stanna hemma". Geometriskt bestämmer vikterna lutningen, eller orienteringen, på neuronens beslutsgräns.
- Det här sista om geometri kanske lät lite klurigt, vi kommer till det snart, du kommer se att ekvationen vi snart kommer skapa kommer bilda en linje genom ett koordinatsystem som skiljer alla möjliga kombinationer som leder till att du går på festen, från de kombinationer som leder till att du inte går på festen.
Bias representerar neuronens grundinställning. Den fungerar som en justerbar tröskel som representerar din grundläggande vilja att gå på fest (positiv bias) eller stanna hemma (negativ bias). Den är alltså partisk mot ett visst beslut.
- Geometriskt bestämmer biasen positionen på beslutsgränsen; den "knuffar" gränsen bort från origo (nollpunkten), vilket ger den friheten att placeras var som helst.

Modellens beräkning är enkel: Summa = (x1*w1) + (x2*w2) + b.

Geometriskt sett är detta mer än bara en summa; ekvationen Summa = 0 definierar en perfekt rak skiljelinje i ett tvådimensionellt rum. Allt på ena sidan linjen är 'Ja', och allt på andra sidan är 'Nej'. När du sätter Summa = 0 kan du lätt skriva om uttrycket som en simpel y = kx + m och rita din raka skiljelinje!

Beslutet fattas sedan av en aktiveringsfunktion: om Summa > 0, blir output 1 (Gå!). Annars blir den 0 (Stanna hemma!). Aktiveringsfunktionen avgör alltså på vilken sida om skiljelinjen din punkt befinner sig på.

En Neuron i Python

Innan vi lär en neuron att lära sig själv, låt oss först bygga själva mekanismen i en Python-klass. Denna Neuron-klass kommer att ha en predict-metod som utför beräkningen. Notera att den inte kan lära sig; istället kommer vi att manuellt ställa in dess vikter och bias för att skapa olika beslutsmodeller.

class Neuron:
    """
    Representerar en enskild, statisk neuron som kan göra en prediktion.
    Denna version kan INTE lära sig. Dess parametrar måste ställas in manuellt.
    """
    def __init__(self, weights, bias):
        # Vikter och bias är "hårdkodade" när vi skapar neuronen.
        self.weights = weights
        self.bias = bias

    def activate(self, value):
        # Aktiveringsfunktionen: om summan är positiv, gissa 1, annars 0.
        if value > 0:
            return 1
        else:
            return 0


    def predict(self, inputs):
        """
        Beräknar den viktade summan och returnerar en prediktion (0 eller 1).
        """
        # Formeln vi implementerar: Summa = (x1*w1) + (x2*w2) + ... + b

        # Låt oss börja på 0
        summation = 0

        # Loopa igenom varje input och dess motsvarande vikt.
        for i in range(len(self.weights)):
            summation += inputs[i] * self.weights[i]

        # Lägg till bias
        summation += self.bias

        return self.activate(summation)

        ```

**Vad händer här?**

- `summation = 0`: Beräkningen av summan börjar alltid på noll.
- `for i in range(len(self.weights)):`: Detta är vår `for`-loop som ersätter matrisberäkning. Den loopar igenom varje input...
- `summation += inputs[i] * self.weights[i]`: ...och multiplicerar den med dess motsvarande vikt, och lägger till resultatet i den totala summan.
- `summation += self.bias`: Slutligen läggs vårt bias till.
- `if summation > 0:`: Detta är vår enkla **aktiveringsfunktion**. Om den totala summan är positiv, "aktiveras" neuronen och returnerar `1`. Annars returnerar den `0`.

Låt oss nu skapa två olika "personligheter" genom att skapa instanser av vår `Neuron`-klass med olika parametrar.

**Persona 1: Den Studiemotiverade**
Denna person prioriterar studier över allt annat. Vänner är trevligt, men ett prov är en deal-breaker.

```python
# Skapa en instans av neuronen för den studiemotiverade.
# Parametrar: weights=[vänner, prov], bias
studious_neuron = Neuron(weights=[0.5, -1.0], bias=-0.2)

# Scenario: Vänner är där (1), men det är ett prov imorgon (1)
inputs = [1, 1]
decision = studious_neuron.predict(inputs)
print(f"Den Studiemotiverade: Input {inputs} -> Beslut: {decision} (Förväntat: 0)")
# Beräkning: (1*0.5) + (1*-1.0) + (-0.2) = -0.7. Resultat: 0 (Stanna hemma)

Persona 2: Sociala Festprissen Denna person älskar att umgås och har en mycket mer avslappnad inställning till prov.

# Skapa en instans för festprissen med andra parametrar.
social_neuron = Neuron(weights=[1.0, -0.1], bias=0.5)

# Samma scenario: Vänner är där (1), prov imorgon (1)
inputs = [1, 1]
decision = social_neuron.predict(inputs)
print(f"Sociala Festprissen: Input {inputs} -> Beslut: {decision} (Förväntat: 1)")
# Beräkning: (1*1.0) + (1*-0.1) + 0.5 = 1.4. Resultat: 1 (Gå på fest!)

Detta visar tydligt hur vikter och bias direkt formar neuronens beslutsfattande. Klassen Neuron och dess predict-metod representerar den grundläggande beräkningsmekanismen.

Men vad händer om vi har 100 inputs istället för 2? Att manuellt hitta de bästa värdena för 100 vikter och en bias blir en omöjlig uppgift. Vi behöver ett sätt för neuronen att hitta de bästa parametrarna själv genom att titta på exempel.

Perceptronen

På 50-talet tog Frank Rosenblatt neuronmodellen och gav den en enkel läranderegel. Kombinationen av neuronmodellen och denna regel är vad som kallas Perceptronen. Regeln låter den lära sig från sina misstag genom en trestegsprocess.

Lärandet behöver en uppsättning träningsdata, vilket innehållet exempel på inputs med motsvarande output - alltså facit.

Perceptronens lärande

För varje exempel i träningsdatan, upprepar Perceptronen följande tre steg:

Gissa: Den tar emot inputs (x1, x2, ...) och beräknar en output (0 eller 1) med hjälp av sina nuvarande vikter och bias.
Beräkna Felet: Den jämför sin gissning med det korrekta svaret (facit). Felet beräknas enkelt: Fel = facit - gissning. Detta kan bara resultera i tre möjliga värden:
- 0: Gissningen var korrekt.
- 1: Gissningen var 0 men borde ha varit 1.
- -1: Gissningen var 1 men borde ha varit 0.
Justera Parametrarna (Lärdom): Om felet var 0 görs ingenting. Om felet var 1 eller -1, justeras alla parametrar för att göra gissningen lite bättre nästa gång. Justeringen följer en enkel formel:
- ny_vikt = gammal_vikt + α * fel * input
- ny_bias = gammal_bias + α * fel

Här är α (alfa) en inlärningsfaktor (ofta ett litet tal som 0.1), som styr hur stora steg lärandet ska ta.

Genom att upprepa dessa tre steg för många exempel, kommer neuronens vikter och bias gradvis att närma sig värden som löser problemet. Låt oss nu se detta i praktiken.

Scenario 1: Du står inför ett beslut. Vännerna är på festen (x1=1) och du har ett prov imorgon (x2=1). Det korrekta beslutet för dig är att stanna hemma och plugga (facit = 0).

Din Perceptron har precis startat och har slumpmässiga startvärden:

w1 (vänner) = 0.5
w2 (prov) = -0.4
b (bias) = 0.0

1. Gissning: Perceptronen räknar: Summa = (1 * 0.5) + (1 * -0.4) + 0.0 = 0.5 - 0.4 = 0.1 Eftersom 0.1 > 0, blir output 1 (Gå på festen).

2. Misstag: Gissningen (1) stämmer inte med facit (0). Du borde ha stannat hemma! Felet är facit - gissning = 0 - 1 = -1.

3. Lärdom: Eftersom felet är negativt, var summan för hög. Perceptronen måste justera sina parametrar för att sänka summan nästa gång den ser en liknande situation. Den använder en enkel uppdateringsregel: ny_parameter = gammal_parameter + inlärningsfaktor * fel * input. Vi sätter inlärningsfaktorn α till 0.1.

w1_ny = 0.5 + 0.1 * (-1) * 1 = 0.4 (Vikten för "vänner" minskar lite)
w2_ny = -0.4 + 0.1 * (-1) * 1 = -0.5 (Vikten för "prov" blir mer negativ)
b_ny = 0.0 + 0.1 * (-1) = -0.1 (Biasen justeras också)

Med de nya parametrarna (w1=0.4, w2=-0.5, b=-0.1), låt oss testa igen: Summa = (1 * 0.4) + (1 * -0.5) - 0.1 = 0.4 - 0.5 - 0.1 = -0.2 Nu är summan negativ, och outputen blir 0. Perceptronen har lärt sig!

Scenario 2: Tänk dig en ny situation. Du är en social person vars grundinställning är att man alltid går på fest om man inte har någon information alls.

Situation: Du vet inget om festen. Inga vänner har sagt något (x1=0) och du har inget prov (x2=0).
Facit: Din grundinställning säger "Gå!" (facit = 1).

Vi använder de senast inlärda vikterna & bias: w1=0.4, w2=-0.5, b=-0.1.

1. Gissning: Summa = (0 * 0.4) + (0 * -0.5) + (-0.1) = -0.1 Eftersom summan inte är större än 0, blir output 0 (Stanna hemma).

2. Misstag: Gissningen (0) stämmer inte med facit (1). Felet är 1 - 0 = 1.

3. Försök till lärdom: Perceptronen justerar nu sina vikter & bias för att höja summan.

w1_ny = 0.4 + 0.1 * (1) * 0 = 0.4 (Ingen ändring!)
w2_ny = -0.5 + 0.1 * (1) * 0 = -0.5 (Ingen ändring!)
b_ny = -0.1 + 0.1 * (1) = 0.0 (Biasen justeras)

Här ser vi varför bias är så viktigt! Biasen är inte beroende av någon input, så den kan alltid justeras om perceptronen beräknat fel svar.

Detta visar hur vikter och bias har två olika men lika viktiga jobb, både mekaniskt och geometriskt.

Vikterna lär sig mönster baserat på den input som finns. Geometriskt justerar de orienteringen (lutningen) på beslutsgränsen.
Biasen lär sig vad neuronens standard-svar ska vara. Geometriskt frigör den beslutsgränsen från origo, vilket låter den justera sin position för att bäst separera datan.

Utan en justerbar bias är neuronens beslutsgräns permanent fastlåst vid nollpunkten och kan bara rotera, vilket gör den oförmögen att lösa många problem.

TODO

illustrera en del olika koordinatsystem som visar skiljelinjers lutning och rotation baserat på vikter och bias.

En Perceptron i Python

Nu när vi förstår teorin är det dags att omsätta den i praktiken. Vi kommer att bygga vår egen Perceptron i Python. För att göra det så tydligt som möjligt bygger vi upp den bit för bit och förklarar varje del.

Vi börjar med att definiera en "mall" eller "ritning" för vår Perceptron med hjälp av en Python-klass.

1. Ritningen: `init` metoden

Först skapar vi själva klassen och dess "konstruktor", __init__. Tänk på __init__ som en funktion som körs automatiskt varje gång vi skapar en ny Perceptron. Dess jobb är att ställa in de grundläggande inställningarna.

# perceptron.py
# importera nödvändiga bibliotek som t.ex. random, numpy, sklearn
import random

class Perceptron:
    """
    En enkel Perceptron-implementation.
    """
    def __init__(self, learning_rate=0.1, n_iterations=10):
        self.learning_rate = learning_rate  # Detta är α (alpha) i vår formel
        self.n_iterations = n_iterations    # Antal gånger vi ska gå igenom träningsdatan
        self.weights = None                 # Vikterna, vi vet inte hur många de är än
        self.bias = None                    # Bias, startar också som okänd

Vad händer här?

class Perceptron:: Vi definierar vår nya ritning.
__init__(self, ...): Detta är konstruktorn.
- learning_rate: Detta är vår inlärningsfaktor (α). Den styr hur stora justeringar vi gör när vi hittar ett fel. Vi ger den ett standardvärde på 0.1.
- n_iterations: Detta tal bestämmer hur många gånger hela träningsdatan ska gås igenom. Att se samma data flera gånger hjälper Perceptronen att finslipa sina vikter.
self.weights = None och self.bias = None: När vi skapar Perceptronen vet den ännu ingenting om datan den ska träna på. Därför vet den inte hur många vikter den behöver (en för varje input-feature) eller vad dess bias ska vara. Vi sätter dem till None för att visa att de är tomma från början.

2. Gissningen: `predict` metoden (Steg 1)

Den första delen av algoritmen: att göra en gissning, är identisk från Neuronen vi tidigare skapade.

3. Lärandet: `fit` metoden (Steg 2 & 3)

Detta är hjärtat i vår Perceptron. fit-metoden är där själva lärandet sker. Den tar emot träningsdatan (inputs och targets) som motsvarar indata och utdata(facit), och kör lärandeloopen för att justera vikter och bias. Fit översätter till anpassa vilket är det vi gör, vi försöker anpassa vikterna efter datat så gott som möjligt.

# (Inuti Perceptron-klassen)

    def fit(self, inputs, targets):
        """
        Tränar Perceptronen genom att iterera över träningsdatan.
        """
        # Steg 0: Initialisering
        # Nu vet vi hur datan ser ut. Vi kan skapa vikterna och bias.

        # Kolla på första exemplet, hur många inputs finns i varje exempel?
        n_inputs = len(inputs[0])

        # Ge varje vikt ett litet slumpmässigt värde, t.ex. mellan -0.5 och 0.5
        self.weights = [random.uniform(-0.5, 0.5) for _ in range(n_inputs)]
        # Vi kan också slumpa biasen, eller börja den på noll. Båda är vanliga.
        self.bias = random.uniform(-0.5, 0.5)

        # Huvudloopen för lärande
        for i in range(self.n_iterations):
            # Gå igenom varje exempel och dess facit
            for input,target in zip(inputs, targets):

                # STEG 1: Gissa (använd metoden vi nyss skapade)
                prediction = self.predict(input)

                # STEG 2: Beräkna Felet
                # error = facit - gissning
                error = target - prediction

                # STEG 3: Justera Parametrar (endast om gissningen var fel)
                if error != 0:
                    # Justera bias: ny_bias = gammal_bias + α * fel
                    self.bias += self.learning_rate * error

                    # Justera varje vikt: ny_vikt = gammal_vikt + α * fel * input
                    for j in range(len(self.weights)):
                        self.weights[j] += self.learning_rate * error * inputs[j]

Vad händer här, steg för steg?

Initialisering: Innan loopen startar, tar vi reda på hur många features varje exempel har (n_features) och skapar en lista med lika många vikter, alla satta till 0.0. Vi sätter också bias till 0.0. Detta är vår startpunkt.
Yttre Loop (for i in range...): Denna loop ser till att vi går igenom hela träningsdatan n_iterations antal gånger.
Inre Loop (for inputs, solution in zip...): Denna loop går igenom varje enskilt tränings-exempel. zip är en praktisk Python-funktion som parar ihop varje inputs med dess motsvarande solution.
Steg 1, 2 och 3: Inuti den inre loopen utför vi exakt de tre stegen från vår teori:
- Vi gör en prediction med den nuvarande kunskapen.
- Vi beräknar ett error genom att jämföra med facit (solution).
- Om error inte är noll, använder vi våra justeringsformler för att uppdatera både bias och alla weights. Notera hur formeln ny_vikt = gammal_vikt + α * fel * input är direkt översatt till koden self.weights[j] += self.learning_rate * error * inputs[j].

Nu har vi alla delar! När vi sätter ihop dem får vi vår kompletta, fungerande Perceptron-klass som är redo att börja lära sig.

Låt oss testa perceptronen i följande tre steg:

Först testar vi den på vårt enkla "fest-scenario" för att bekräfta att den fungerar som förväntat.
Sedan tar vi steget till ett klassiskt, verkligt dataset (Iris) för att se hur den hanterar riktig data.
Slutligen jämför vi vår hemmabyggda Perceptron med den professionella versionen som finns i ett av de mest populära maskininlärningsbiblioteken, Scikit-learn.

Steg 1: Test på vårt "fest-scenario"

Låt oss börja med att applicera vår nyskapade Perceptron på det problem vi känner till bäst. Målet är att den ska lära sig logiken: "gå på fest, om du inte har ett prov".

# --- Användning av vår Perceptron ---

# 1. Definiera vår träningsdata med beskrivande namn.
# 'training_examples' innehåller inputs [[vänner, prov], ...]
inputs = [
    [0, 0],  # Inga vänner, inget prov
    [0, 1],  # Inga vänner, prov
    [1, 0],  # Vänner, inget prov
    [1, 1]   # Vänner, prov
]

# 'training_solutions' innehåller motsvarande facit.
targets = [1, 0, 1, 0] # 1 = Gå, 0 = Stanna hemma

# 2. Skapa en instans av vår Perceptron.
perceptron = Perceptron(learning_rate=0.1, n_iterations=5)

# 3. Kör träningen.
# Vi matar in exemplen och facit i vår .fit()-metod.
perceptron.fit(inputs,targets)

# 4. Granska resultatet.
print(f"\nSlutgiltiga inlärda vikter: {perceptron.weights}")
print(f"Slutgiltig inlärd bias: {perceptron.bias}")

# 5. Testa den färdigtränade modellen.
print("\n--- Testar den tränade modellen ---")
test_fall_1 = [1, 1]  # Vänner är där, prov imorgon
test_fall_2 = [1, 0]  # Vänner är där, inget prov

print(f"Inputs: {test_fall_1} -> Prediktion: {perceptron.predict(test_fall_1)} (Förväntat: 0)")
print(f"Inputs: {test_fall_2} -> Prediktion: {perceptron.predict(test_fall_2)} (Förväntat: 1)")

Analys av resultatet:

När du kör koden kommer du se hur vikterna och biasen justeras för varje iteration. Det slutgiltiga resultatet kommer troligen att visa:

En negativ vikt för den andra inputen (w2, provet). Detta betyder att ett prov starkt talar emot att gå på fest.
En vikt nära noll för den första inputen (w1, vänner). Modellen har lärt sig att denna faktor inte är avgörande för beslutet i detta specifika dataset.
En positiv bias. Detta representerar en grundinställning att "gå på fest" om inga andra starka skäl (som ett prov) finns.

Modellen har alltså framgångsrikt lärt sig den logiska regeln från datan!

Steg 2: Perceptronen på ett riktigt dataset (Iris)

Nu tar vi steget från ett påhittat problem till ett verkligt. Vi ska använda det berömda Iris-datasetet, som innehåller mätningar av tre olika arter av Iris-blommor.

En viktig begränsning med vår enkla Perceptron är att den är en binär klassificerare, vilket betyder att den bara kan svara på frågor med två möjliga utfall (som 0 eller 1, Ja eller Nej). Iris-datasetet har tre arter, så vi måste förenkla problemet: "Är denna blomma en Iris-Setosa, eller inte?"

Vi kommer också bara att använda två av de fyra tillgängliga måtten (features/inputs) för att hålla det enkelt.

Notera att det är vanligt att vi kallar inputs för X och targets för y.

# Vi behöver ladda in datasetet, vilket vi gör med hjälp av biblioteket Scikit-learn.
# Vi behöver ladda in datasetet och nya verktyg
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 1. Ladda och förbered datan
iris = load_iris()

# Välj alla rader, och välj första 2 kolumnerna i varje rad.
# de features eller inputs vi tränar på för varje blomma är sepal length och width
X = iris.data[:, :2]

# skapa facit, 1 om target == 0, annars 0
# target är 0,1,2 för setosa, versicolor, verginica
y = (iris.target == 0).astype(int)

# 2. DELA UPP DATAN
# Vi delar upp X och y i tränings- och test-set.
# test_size=0.3 betyder att 30% av datan blir testdata.
# random_state=1337 säkerställer att vi får samma "slumpmässiga" uppdelning varje gång vi kör koden.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1337)

print(f"Storlek på träningsdata: {len(X_train)} exempel")
print(f"Storlek på testdata: {len(X_test)} exempel\n")

# 3. Skapa och träna en Perceptron-instans PÅ TRÄNINGSDATAN
iris_perceptron = Perceptron(learning_rate=0.1, n_iterations=10)
iris_perceptron.fit(X_train, y_train) # Tränar bara på _train

# 4. Gör prediktioner och utvärdera PÅ TESTDATAN
predictions = [iris_perceptron.predict(inputs) for inputs in X_test]
accuracy = accuracy_score(y_test, predictions) # Jämför med facit för _test

print(f"\n--- Test på Iris-datasetet (med Train/Test Split) ---")
print(f"Noggrannhet på testdatan: {accuracy * 100:.2f}%")

Analys av resultatet:

Du kommer att se att vår enkla Perceptron uppnår mycket imponerande noggrannhet på detta problem! Detta beror på att Iris Setosa-blommorna är så pass olika de andra två arterna (baserat på dessa två features) att det går att dra en perfekt rak linje mellan dem. Detta kallas att datan är linjärt separerbar, vilket är det ideala scenariot för en Perceptron.

Steg 3: Jämförelse med Scikit-learn

Vi har byggt vår Perceptron för att förstå hur den fungerar. I praktiken använder man nästan alltid färdiga, optimerade och robusta implementationer från bibliotek som t.ex. Scikit-learn. Låt oss se hur man löser exakt samma problem med deras version.

Lägg märke till hur lika kodstrukturen är! Metoderna heter också .fit() och .predict(), vilket är en standard som Scikit-learn använder för alla sina modeller.

# Importera den professionella Perceptron-modellen från Scikit-learn
from sklearn.linear_model import Perceptron as SklearnPerceptron

# 1. Skapa en instans av Scikit-learns Perceptron
# Notera: Vi behöver inte ange learning_rate eller n_iterations,
# den har inbyggda standardvärden och smartare sätt att avgöra när den är färdigtränad.
sk_perceptron = SklearnPerceptron()

# 2. Träna modellen (ser identiskt ut!)
sk_perceptron.fit(X, y)

# 3. Gör prediktioner och utvärdera
sk_predictions = sk_perceptron.predict(X)
sk_accuracy = accuracy_score(y, sk_predictions)

print(f"\n--- Test med Scikit-learns Perceptron ---")
print(f"Noggrannhet med Scikit-learns Perceptron: {sk_accuracy * 100:.2f}%")

Slutsats av jämförelsen:

Resultatet är detsamma (100% noggrannhet), men koden för att använda den färdiga modellen är kortare och den underliggande implementationen är mycket mer effektiv och full av extra funktioner.

Genom att först bygga vår egen Perceptron har vi fått en djup förståelse för vad som händer när vi anropar sk_perceptron.fit(X, y). Vi förstår nu logiken med vikter, bias, inlärningsfaktor och iterationer som ligger gömd bakom den enkla funktionen. Detta är den sanna styrkan med att bygga saker från grunden: det avmystifierar verktygen som experterna använder varje dag.

Perceptronens svaghet

Optimismen var enorm. Men den krossades 1969 när AI-pionjärerna Marvin Minsky och Seymour Papert publicerade boken "Perceptrons". I den bevisade de matematiskt att en enskild Perceptron hade en fundamental, inbyggd begränsning.

Problemet är att en enskild neuron, med sin beräkning (w1*x1) + (w2*x2) + ... + b, är matematiskt begränsad till att skapa en linjär besutsgräns. I vårt tvådimensionella problem är denna gräns en perfekt rak linje. I ett tredimensionellt problem är det ett platt plan. I N dimensioner är det ett (N-1)-dimensionellt "hyperplan".

Lärningsprocessen handlar om att hitta den bästa lutningen (vikterna) och positionen (biasen) för denna linje, men den kan aldrig förvandla linjen till en kurva, en cirkel eller någon annan form.

Vad händer med ett lite mer komplext beslut?

Låt oss bygga vidare på vårt "Ska jag gå på festen?"-exempel. Dina två inputs är nu:

x1: Är Ron på festen? (1 för Ja, 0 för Nej)
x2: Är Hermione på festen? (1 för Ja, 0 för Nej)

Din beslutsregel är lite komplicerad. Du vill gå om en av dem är där, men du vill inte gå om ingen är där (tråkigt) och du vill absolut inte gå om båda är där (för att undvika att bli ett femte hjul).

Detta är ett klassiskt logiskt problem som kallas XOR ("antingen eller, men inte båda"). Låt oss översätta din regel till siffror, där 1 är "Gå!" och 0 är "Stanna hemma!":

Ron är INTE där (0) och Hermione är INTE där (0) → Stanna hemma (0).
Ron ÄR där (1) och Hermione är INTE där (0) → Gå! (1).
Ron är INTE där (0) och Hermione ÄR där (1) → Gå! (1).
Ron ÄR där (1) och Hermione ÄR där (1) → Stanna hemma (0).

Låt oss plotta dessa möjliga utfall på en 2D-graf. Rons närvaro är x-axeln och Hermiones närvaro är y-axeln. Vi använder en grön cirkel för "Gå!" och ett rött kryss för "Stanna hemma!".

Du får då fyra punkter:

En punkt vid (0, 0) som är ett rött kryss.
En punkt vid (1, 0) som är en grön cirkel.
En punkt vid (0, 1) som är en grön cirkel.
En punkt vid (1, 1) som är ett rött kryss.

Den omöjliga linjen Utmaningen är nu: Kan en Perceptron hitta en uppsättning vikter w1, w2 (linjens lutning) och en bias b (linjens position) så att linjen w1*x1 + w2*x2 + b = 0 perfekt separerar de gröna cirklarna från de röda kryssen?

TODO

Illustration: Fest-dilemmat (XOR-problemet). Rita en 2D-graf med axlarna "Är Ron där?" och "Är Hermione där?", där varje axel bara har punkterna 0 och 1.

Rita ett rött kryss vid koordinaten (0, 0) och märk det "Stanna hemma".
Rita en grön cirkel vid koordinaten (1, 0) och märk det "Gå!".
Rita en grön cirkel vid koordinaten (0, 1) och märk det "Gå!".
Rita ett rött kryss vid koordinaten (1, 1) och märk det "Stanna hemma".
Rita en streckad linje för att visa ett misslyckat försök att separera cirklarna från kryssen. Skriv en bildtext: "Det är omöjligt att separera de tillfällen man vill gå från de man vill stanna hemma med en enda rak linje."

Titta på grafen. Det är geometriskt omöjligt.

En horisontell linje? Separerar inte.
En vertikal linje? Separerar inte.
En diagonal linje? Den kommer alltid att ha en grön cirkel och ett rött kryss på fel sida.

Detta var Minsky och Paperts bevis. De visade att eftersom en Perceptron bara kan lära sig linjära separationer, kunde den inte ens lösa detta grundläggande sociala dilemma. Perceptronens matematiska verktyg – den raka linjen – var helt enkelt inte tillräckligt sofistikerat för problemet. Slutsatsen de drog: om denna modell inte ens klarar av att bestämma om man ska gå på en fest, hur ska den då någonsin kunna efterlikna den komplexa mänskliga hjärnan?

Det påstås att denna kritik var bidragande till att forskning inom AI koncentrerades till symbolisk AI, vilket som vi redan nämnt ledde oss in i den första "AI-vintern".

Men hallå, chilla gorilla, 2 sekunder bara.

Visserligen är det tydligt att en perceptron inte kan modellera en XOR operation. Men vi kan enkelt modellera NAND eller NOR operationerna.

TODO

insert tabell + graf över nand & nor

Något spännande med dessa två är deras unika egenskap att de kan användas för att realisera alla andra logiska funktioner. Det är alltså möjligt att bygga en XOR eller vilken annan logisk funktion som helst med hjälp av endast NAND-grindar eller endast NOR-grindar.

TODO

illustrera hur XOR kan representeras som 4stycken NAND grindar (perceptrons som lärt sig NAND)

Så flera perceptroner sammanlänkade kan alltså representera mer avancerade mönster? Coolt!

Och hur var det med riktiga neuroner? Den mänskliga hjärnan som är väldigt komplex består av ett enormt nätverk av sammankopplade neuroner... Känns det som att det kanske ändå fanns ett spår framåt här som förtjänade att utforskas...?

Neurala Nätverk

Några få forskare vägrade ge upp. De insåg att problemet inte var neuronen i sig, utan att man bara använde en. Våra hjärnor har miljarder neuroner. Vad skulle hända om man, precis som i hjärnan, kopplade ihop massor av dem i lager? Detta skapar vad vi kallar ett Neuralt Nätverk.

Ett neuralt nätverk består vanligtvis av tre typer av lager:

Input-lager: Tar emot den initiala datan. Varje neuron representerar en del av datan (t.ex. en pixel i en bild).
Dolda lager (Hidden Layers): Ett eller flera mellanliggande lager. Här sker det verkliga "tänkandet". Magin ligger i att varje lager lär sig att känna igen mönster från det föregående lagret, vilket skapar en hierarki av kunskap.
Output-lager: Producerar det slutgiltiga svaret (t.ex. "Detta är en bild på en katt").

TODO

illustrera ett simpelt nätverk

Steg för steg: Hur ett nätverk lär sig känna igen siffran "4"

Låt oss följa datan genom ett enkelt nätverk som ska känna igen handskrivna siffror. Input är en liten bild, 28x28 pixlar, av siffran "4".

Steg 1: Input-lagret Nätverket har 784 neuroner i sitt input-lager (28 * 28 = 784). Varje neuron tar emot värdet från en enda pixel – kanske 1 för en svart pixel och 0 för en vit. Detta lager "ser" bara en massa osammanhängande punkter.

TODO

Illustration: Input-lagret. Visa en bild av en handskriven "4" på ett rutnät. Rita sedan en kolumn av cirklar (neuroner) bredvid, och visa hur varje pixel mappas till en neuron i input-lagret.

Steg 2: Första Dolda Lagret – Hitta enkla former Neuronerna i detta lager får sina inputs från alla neuroner i input-lagret. Genom träning (som vi kommer till) har de specialiserat sig.

Neuron A i detta lager kanske har lärt sig att "avfyra" starkt när den ser en kort, vertikal linje i det övre vänstra hörnet. Den har utvecklat höga positiva vikter för pixlarna i just det området och låga eller negativa vikter för alla andra.
Neuron B har lärt sig att känna igen en horisontell linje i mitten.
Neuron C har lärt sig att känna igen en lång, vertikal linje till höger.

När bilden av en "4" matas in, kommer Neuron A, B och C alla att avfyra starkt, medan en neuron som letar efter en cirkel (som i en "8" eller "0") kommer att vara tyst. Outputen från detta lager är alltså inte längre pixlar, utan en samling koncept: "ja, det finns en vertikal linje här", "ja, det finns en horisontell linje där".

TODO

Illustration: Första dolda lagret. Visa bilden av en "4". Rita sedan tre exempelneuroner från det dolda lagret. Från den första, rita linjer till pixlarna i den korta vertikala delen av "4:an" och färglägg dem. Gör likadant för de andra två neuronerna och deras respektive delar av siffran.

Steg 3: Andra Dolda Lagret (eller Output-lagret) – Kombinera formerna Neuronerna i detta lager får sina inputs från neuronerna i det föregående lagret. De lär sig att känna igen kombinationer av de enkla formerna.

Det finns en neuron i output-lagret för varje möjlig siffra (0-9).
"Fyra"-neuronen har lärt sig att den ska avfyra om den får starka signaler från de neuroner i föregående lager som känner igen "kort vertikal linje uppe till vänster", "horisontell linje i mitten" OCH "lång vertikal linje till höger". Den har alltså höga positiva vikter kopplade till just Neuron A, B och C.
"Etta"-neuronen har istället lärt sig att den bara behöver en stark signal från Neuron C (lång vertikal linje).

Eftersom bilden av en "4" aktiverade A, B och C, kommer "Fyra"-neuronen att få en mycket hög summerad input och avfyra med högsta sannolikhet. Nätverkets svar blir: "Jag är 99% säker på att detta är en 4".

Men okej, vänta lite här. 99% ?! starka signaler? Hittills har vi bara diskuterat 1 eller 0 som input/output.

Vår perceptron behöver få några uppgraderingar till.

Idén att kombinera flera enkla enheter för att lösa komplexa problem är själva kärnan i neurala nätverk. Men innan vi börjar bygga nätverk av Perceptroner, finns det en annan fundamental begränsning vi måste adressera hos vår enskilda neuron: dess digitala natur.

Hittills har vår modell levt i en binär värld:

Input: "Är vänner där?" (1 eller 0).
Output: "Gå på festen!" (1 eller 0).

Men verkligheten är sällan så svartvit.

Variationer i input

Tänk om vår input inte var en ja/nej-fråga, utan en gradvis skala?

Istället för "Är vänner där?", kanske frågan är "Hur många vänner är där?" (en siffra som 0, 1, 5, 10...).
Istället för "Har jag ett prov imorgon?", kanske det är "Hur svårt är provet på en skala 1-10?".
Om du redan gjort pingvinuppgiften så är input längden på pingvinens

Den goda nyheten är att vår neurons beräkning av vikterna, Summa = (x1*w1) + (x2*w2) + b, hanterar detta utan problem. Vikterna (w) fungerar fortfarande som en justerbar "viktighet" för varje input, oavsett om inputen är 0.75 eller 100. Den matematiska grunden är alltså redan flexibel nog för att hantera icke-binär input.

Variationer i output

Även informationen som neuronen skickar vidare skulle kunna vara något annat än 1 eller 0.

Ska neuronen skicka något annat behöver vi uppdatera vår aktiveringsfunktion. Just nu använder vi en enkel stegfunktion: om summan är större än noll blir resultatet 1, annars 0. Det är en "allt eller inget"-mekanism.

Men tänk om vi vill förutsäga något som inte är ett simpelt ja/nej-beslut?

Vad är sannolikheten för att det kommer att regna imorgon (ett tal mellan 0.0 och 1.0)?
Vad kommer ett hus att kosta (ett positivt, kontinuerligt värde)?

Här behöver vi ersätta den hårda stegfunktionen med något mjukare. Istället för en tröskel som abrupt slår om från 0 till 1, kan vi använda en funktion som skapar en mjuk, gradvis övergång.

En av de mest klassiska "mjuka" aktiveringsfunktionerna är sigmoid-funktionen. Den tar vilket tal som helst (från minus oändligheten till plus oändligheten) och "klämmer ihop" det till ett värde mellan 0 och 1.

Efter att vi summerat samtliga inputs multiplicerat med sina respektive inputs och lagt till bias, används aktiveringsfunktionen.

Såhär ser vår stegfunktion ut som har ett binärt output.

def activate(self, value):
    return value > 0 # över eller under skiljelinjen?

Sigmoid-funktionen ser ut såhär:

def activate(self, value):
    return 1 / (1 + math.exp(-value))  # kläm ihop mellan 0 och 1

och såhär ser de ut om vi plottar funktionen på en graf:

TODO

Illustration: Stegfunktion vs. Sigmoid-funktion. Rita två grafer sida vid sida.

Vänster graf: Visa den klassiska stegfunktionen. En linje vid y=0 som abrupt hoppar till y=1 vid x=0. Bildtext: "Stegfunktionen: Output är antingen 0 eller 1. Ett hårt, binärt beslut."
Höger graf: Visa en S-formad kurva (Sigmoid) som mjukt går från nära 0 till nära 1 och passerar 0.5 vid x=0. Bildtext: "Sigmoid-funktionen: Output är ett värde mellan 0 och 1. Perfekt för att representera en sannolikhet."

Denna lilla förändring – att byta ut stegfunktionen mot en mjukare, differentierbar funktion som Sigmoid – är en av de mest avgörande uppgraderingarna av Perceptron-modellen. Det ger neuronen två superkrafter:

Den kan ge nyanserade svar: Istället för "Ja" kan den säga "87% chans".
Den ger bättre feedback för lärande: Eftersom funktionen är mjuk, kan vi se hur nära vi var ett korrekt beslut. Om gissningen var 0.6 och facit 1.0, var felet mindre än om gissningen var 0.1. Denna nyans är kritisk för de mer avancerade inlärningsalgoritmer som moderna neurala nätverk använder.

Genom att uppgradera vår enskilda neuron till att hantera kontinuerliga värden och använda en mjuk aktiveringsfunktion, har vi skapat en mer kraftfull och flexibel byggsten.

Coolt! Men alltså... Hur förstog varje perceptron hur den skulle uppdatera sina vikter? Tidigare fick en perceptron jämföra sitt svar med ett facit. Om svaret från output lagret är det som jämförs med facit.. hur kan då enskilda perceptroner i någon av de gömda lagren lära sig? :O

Detta är känt som "The Credit Assignment Problem" (ungefär "problemet med att fördela beröm och skuld"). Om nätverket gissar fel, vilka av de tusentals neuronerna och miljontals kopplingarna bär ansvaret?

Backpropagation

Den geniala lösningen kom 1986 med en teknik kallad Backpropagation ("bakåtpropagering av fel").

Nedan är en översiktlig beskrivning, sedan kommer en mer fördjupad: Vi matar in bilden av en "4", men nätverkets nuvarande vikter är dåliga, så den neuron som lyser starkast i output-lagret är "9"-neuronen. Den är 90% säker på att det är en nia. "4"-neuronen är bara 5% säker.

Felet är uppenbart. Nu börjar backpropagation-processen, som sker i två steg baklänges genom nätverket:

Steg 1: Skuldfördelning i sista lagret Algoritmen tittar på output-lagret och konstaterar:

Till "9"-neuronen: "Du skulle ha varit tyst (0), men du skrek högt (0.9). Ditt fel är stort och för högt. Du var för självsäker."
Till "4"-neuronen: "Du skulle ha skrikit högt (1), men du viskade bara (0.05). Ditt fel är stort och för lågt. Du var för osäker."
Till de andra neuronerna (0, 1, 2, 3, 5, 6, 7, 8): "Ni var ganska tysta, vilket var rätt. Ert fel är litet."

Steg 2: En kedjereaktion av justeringar bakåt Nu börjar den verkliga magin. Varje felaktig neuron tittar "bakåt" på de kopplingar (vikter) och neuroner i det föregående lagret som gav den sin input.

"9"-neuronen resonerar så här: "Jag aktiverades för starkt. Vilka av mina inkommande signaler var starkast? Aha, det var från neuronerna i det dolda lagret som känner igen 'en cirkel högst upp' och 'en lång vertikal linje'. De bidrog mest till mitt misstag. För att jag ska göra mindre fel nästa gång, måste jag lita mindre på dem."
- Åtgärd: Algoritmen sänker vikten på kopplingen mellan "cirkel-neuronen" och "9"-neuronen. Den gör samma sak för "lång-vertikal-linje-neuronen".
"4"-neuronen resonerar samtidigt: "Jag aktiverades för svagt. Jag borde ha lyssnat mer på de neuroner som faktiskt signalerade korrekt. Aha, neuronerna för 'kort vertikal linje', 'horisontell linje' och 'lång vertikal linje' var alla aktiva. Deras bidrag var korrekt, men jag ignorerade dem."
- Åtgärd: Algoritmen höjer vikten på kopplingarna från dessa tre ingående neuronerna till "4"-neuronen.

Denna skuldfördelning fortsätter sedan bakåt. "Cirkel-neuronen" (som felaktigt bidrog till en "9:a") får nu själv en "skuldsignal" och resonerar: "Okej, jag aktiverades för starkt. Vilka pixlar i input-bilden var det som fick mig att aktiveras? Jag måste sänka vikterna från dem."

Många bäckar små

Varje enskild justering är pytteliten. Men processen upprepas för tusentals, ibland miljontals, exempelbilder. För varje bild gör nätverket en gissning, beräknar felet och skickar en våg av pyttesmå korrigeringar bakåt genom hela systemet.

Det är denna eleganta, matematiska process av att fördela skuld baklänges och göra små, ständiga justeringar som gör att ett nätverk kan gå från att gissa slumpmässigt till att klassificera bilder med övermänsklig precision. Plötsligt var vägen öppen för att bygga de djupt komplexa och kraftfulla inlärningssystem vi ser idag.

TODO

Illustration: Hela nätverket. En översiktsbild som visar:

Input-lagret (en matris av neuroner som representerar "4:an").
Pilar till Första Dolda Lagret, där några neuroner är upplysta (de som känner igen kanter/linjer i "4:an").
Pilar till Output-lagret (10 neuroner, 0-9), där endast neuronen för "4" är starkt upplyst.
En böjd pil märkt "Backpropagation" som går från output bakåt genom nätverket, för att visa hur felet justerar vikterna.

Träning av Neurala Nätverk

Perceptronens läranderegel var elegant i sin enkelhet, men den fungerar inte för ett nätverk med flera lager. Dels för att våra nya neuroner ger nyanserade svar (t.ex. 0.87 istället för 1), men framför allt på grund av problemet med skuldfördelning: hur vet en neuron i ett dolt lager om den gjorde "rätt" eller "fel"?

För att lösa detta krävs en mer sofistikerad, tvådelad process: Gradient Descent som övergripande strategi för att hitta de bästa vikterna, och Backpropagation som den mekanism som gör strategin möjlig.

Gradient Descent

När nätverket gissar fel uppstår en total kostnad (felet). Denna kostnad är beroende av alla vikter i hela nätverket tillsammans. Ändrar vi en enda vikt litegrann, så kommer den totala kostnaden att förändras. Målet är att justera nätverket så att vi närmar oss en kostnad på 0(inget fel!).

Kostnaden kan alltså ses som en funktion av vikterna! Gradient Descent är strategin vi använder för att hitta den kombination av vikter som ger lägst möjliga kostnad. Strategin är super-simpel! För varje enskild vikt behöver vi bara räkna ut åt vilket håll den påverkar den totala kostnaden och hur mycket – alltså inspektera lutningen.

Denna lutning kallas för gradienten.

Om lutningen är brant (hög gradient) betyder det att vi har mycket att vinna på att ändra vikten. Vi tar då ett större kliv nedåt för att snabbt minska felet. Om lutningen däremot är flack (låg gradient) är vi antagligen nära botten av dalen. Då blir våra steg automatiskt mindre, vilket är perfekt för att finjustera vikten den sista lilla biten utan att råka hoppa förbi målet.

Den observante läsaren förstår förstås att denna simpla strategi skulle kunna göra att vi fastnar i en liten grop på vägen ner (ett så kallat lokalt minimum) istället för att hitta den allra djupaste botten, men mer om alternativa lösningar senare. Det här funkar GOOD ENOUGH just nu!

Vår uppdateringsregel för varje enskild vikt blir:

ny_vikt = gammal_vikt - α * gradienten_för_denna_vikt

Här är α vår inlärningsfaktor (som bestämmer grundtakten). gradienten_för_denna_vikt är svaret på frågan: "Om jag ökar just denna vikt, hur mycket ökar eller minskar den totala kostnaden då?"

I koden är det just denna gradient vi räknar ut när vi multiplicerar neuronens felansvar (delta) med dess inkommande signal (input). Att göra detta effektivt för miljontals vikter, där många ligger djupt inne i nätverket, är den verkliga utmaningen som löses med nästa steg: backpropagation.

Backpropagation

Backpropagation är en algoritm för att beräkna gradienten för varje vikt. Den gör detta genom att först beräkna ett "felansvar" för varje enskild neuron. Olika neuroner kommer alltså vara olika ansvariga för eventuella fel i nätverket. Givet ett fel i slutet, behöver vi hitta vilka som var mest bidragande till felet, och korrigera deras vikter mest!

Detta felansvar kallar vi för delta (δ). När vi vet varje neurons delta, blir det enkelt att räkna ut gradienten för dess inkommande vikter.

Processen för ett enskilt tränings-exempel sker alltid i fyra steg:

Steg 1: Framåtpasset (Prediction) Först skickar vi in vår data och låter den flöda framåt genom nätverket, lager för lager, tills vi får en slutgiltig gissning. Under detta steg är det avgörande att vi sparar alla outputs från varje enskild neuron. Vi kommer att behöva dem i de kommande stegen.

I koden: Detta motsvarar den första delen av .fit()-metoden, där vi fyller listan outputs_by_layer.

Steg 2: Felansvar (Delta) för Output-lagret Nu börjar vi bakifrån. För varje neuron i det allra sista lagret kan vi direkt beräkna dess felansvar (delta). Formeln är:

δ_output = (facit - gissning) * derivatan_av_aktiveringsfunktionen(gissning)

Låt oss bryta ner det:

(facit - gissning): Detta är det uppenbara felet. Om gissningen var 0.7 och facit 1.0, är felet 0.3.
derivatan_av_aktiveringsfunktionen(...): Den svarar på frågan: "Hur känslig var neuronens output för ändringar i sin summerade input?". Om neuronen gav en output på 0.99 är den nästan "mättad" och dess aktiveringsfunktion är väldigt platt. Då blir derivatan nära noll, vilket gör delta litet – neuronen hade inte kunnat ändra sig så mycket ändå.
- Vi tilldelar alltså ett högt felansvar (delta) till de neuroner som gjorde fel och vars output har möjlighet att ändra sig genom att skruva på vikterna
I koden: Detta är den första for-loopen i backpropagation-delen, där vi beräknar output_deltas. error i koden är (facit - gissning).

Steg 3: Felansvar (Delta) för Dolda Lager Detta är kärnan i backpropagation. För att beräkna delta för en neuron i ett dolt lager, tittar vi "framåt" på de deltas vi just beräknade i nästa lager. Formeln är:

δ_dold = (summerat fel från nästa lager) * derivatan_av_aktiveringsfunktionen(dold_neurons_output)

Låt oss bryta ner den första, viktigaste delen:

(summerat fel från nästa lager): För att beräkna detta, frågar vår dolda neuron varje neuron i lagret framför: "Vad var ditt delta, och hur stark var kopplingen (vikten) mellan oss?". Den multiplicerar dessa två värden för varje koppling framåt och summerar resultatet. Detta är en viktad summa av felansvaret från nästa lager.
I koden: Detta motsvarar den näst sista for-loopen. Variabeln error_contribution är exakt denna summering. Den samlar in skulden från nästa lager, viktat av styrkan på kopplingarna.

Steg 4: Beräkna Justeringar och Uppdatera Vikter & Biaser Nu när vi har delta (felansvaret) för varje neuron i hela nätverket, är det sista steget att beräkna hur mycket varje parameter ska justeras.

Justering av Vikter: Gradienten (lutningen) för en specifik vikt som går från Neuron X (med output O_X) till Neuron Y (med delta δ_Y) är:

gradient_för_vikt = δ_Y * O_X

Intuitivt: en vikts justering ska vara som störst om...

...neuronen den leder till hade ett stort felansvar (δ_Y är stort).
...signalen som passerade genom vikten var stark (O_X är stort).

Om signalen var noll, hade vikten inget inflytande och dess justering blir noll, oavsett hur stort felet var. Felet ligger alltså hos någon av de andra vikterna. Ändrar vi på den här vikten så ändras inte felet i den riktning vi vill ändra felet.

Justering av Bias: Och hur uppdateras biasen? Det är ännu enklare. Biasen är inte kopplad till någon föregående neurons output. Det bästa sättet att tänka på den är som en vikt som är kopplad till en "fiktiv" input som alltid har värdet 1.

Om vi använder samma formel som för en vanlig vikt blir gradienten för biasen:

gradient_för_bias = δ_Y * 1 = δ_Y

Gradienten för en neurons bias är alltså helt enkelt neuronens eget delta! Den påverkas inte av vad som kom in i neuronen, bara av neuronens totala felansvar.

Uppdateringsregeln: Nu kan vi använda dessa gradienter för att justera våra parametrar. Justeringen vi gör är:

justering = inlärningsfaktor * gradient

Och vi lägger till denna justering till våra gamla vikter och biaser:

ny_vikt = gammal_vikt + α * (δ_Y * O_X) ny_bias = gammal_bias + α * δ_Y

I koden: Detta är den allra sista, nästlade for-loopen.
- delta är δ_Y.
- input_val (eller inputs_to_layer[k]) är O_X.
- Raden neuron.weights[k] += learning_rate * delta * input_val implementerar exakt uppdateringen för vikten.
- Raden neuron.bias += learning_rate * delta implementerar den enklare uppdateringen för biasen.

Genom att upprepa dessa fyra steg tusentals gånger, justeras alla vikter och biaser i nätverket gradvis för att minimera den totala kostnaden.

Ett Neuralt Nätverk i Python

Nu när vi har en detaljerad förståelse för algoritmen, blir koden en direkt översättning av dessa steg.

Byggstenen: En Passiv Neuron

import numpy as np
import math

class Neuron:
    """En passiv neuron som bara kan göra en prediktion."""
    def __init__(self, num_inputs):
        # Ge varje vikt ett litet slumpmässigt värde, t.ex. mellan -0.5 och 0.5
        self.weights = [random.uniform(-0.5, 0.5) for _ in range(n_inputs)]
        # Vi kan också slumpa biasen, eller börja den på noll. Båda är vanliga.
        self.bias = random.uniform(-0.5, 0.5)

    def _sigmoid(self, x):
        if x < -700: return 0.0
        return 1 / (1 + math.exp(-x))

    def _sigmoid_derivative(self, sig_output):
        return sig_output * (1 - sig_output)

    def predict(self, inputs):
        """Beräknar (x1*w1 + x2*w2 + ...) + b"""
        total = 0
        for i in range(len(self.weights)):
            total += inputs[i] * self.weights[i]
        total += self.bias
        return self._sigmoid(total)

Tränaren: Nätverket

import numpy as np
import random
import math

class NeuralNetwork:
    """Ett nätverk som kan tränas med Backpropagation."""
    def __init__(self, layer_sizes):
        """
        layer_sizes: En lista som anger antalet neuroner i varje lager.
        T.ex. [2, 3, 1] betyder:
        - Input lager: 2 noder (dessa är bara passiva inputs)
        - Dold lager 1: 3 neuroner
        - Output lager: 1 neuron
        """
        self.layers = []
        # Skapa neuroner för varje lager (utom input-lagret som inte har neuroner)
        for i in range(1, len(layer_sizes)):
            num_inputs = layer_sizes[i-1] # Inputs kommer från föregående lager
            num_neurons = layer_sizes[i]
            # Skapa ett lager med 'num_neurons', där varje neuron lyssnar på 'num_inputs'
            self.layers.append([Neuron(num_inputs) for _ in range(num_neurons)])

    def predict(self, inputs):
        """Kör datan framåt genom nätverket."""
        current_inputs = inputs
        for layer in self.layers:
            # Låt varje neuron i lagret göra sin gissning
            next_inputs = [neuron.predict(current_inputs) for neuron in layer]
            current_inputs = next_inputs
        return current_inputs

    def fit(self, training_examples, training_solutions, epochs, learning_rate):
        """
        Tränar nätverket.
        VIKTIGT: training_solutions måste vara One-Hot encoded om du har flera outputs!
        T.ex. för klass 2 av 3: [0, 1, 0]
        """
        for epoch in range(epochs):
            for inputs, solution in zip(training_examples, training_solutions):

                # --- STEG 1: FRAMÅTPASS (Forward Pass) ---
                # Vi måste spara output från VARJE lager för att kunna köra backprop senare.
                outputs_by_layer = [inputs]
                current_inputs = inputs
                for layer in self.layers:
                    next_inputs = [n.predict(current_inputs) for n in layer]
                    outputs_by_layer.append(next_inputs)
                    current_inputs = next_inputs

                # --- STEG 2: BAKÅTPASS (Backpropagation) ---
                deltas = []

                # A. Beräkna fel för OUTPUT-LAGRET
                final_outputs = outputs_by_layer[-1]
                output_deltas = []
                # För varje output-neuron, jämför med facit (solution)
                for i, neuron in enumerate(self.layers[-1]):
                    # Felet = Facit - Gissning
                    error = solution[i] - final_outputs[i]
                    # Delta = Felet * Derivatan (hur känslig är neuronen just nu?)
                    delta = error * neuron._sigmoid_derivative(final_outputs[i])
                    output_deltas.append(delta)
                deltas.append(output_deltas)

                # B. Beräkna fel för DOLDA LAGER (Baklänges)
                # Vi loopar baklänges från näst sista lagret till första
                for i in range(len(self.layers) - 2, -1, -1):
                    current_deltas = []
                    layer = self.layers[i]
                    next_layer = self.layers[i+1]

                    for j, neuron in enumerate(layer):
                        # Hur mycket bidrog denna neuron till felen i nästa lager?
                        error_contribution = 0
                        for k, next_neuron in enumerate(next_layer):
                            # (Felet hos nästa neuron) * (Vikten som kopplar ihop dem)
                            error_contribution += deltas[0][k] * next_neuron.weights[j]

                        neuron_output = outputs_by_layer[i+1][j]
                        delta = error_contribution * neuron._sigmoid_derivative(neuron_output)
                        current_deltas.append(delta)

                    # Lägg till deltas först i listan (eftersom vi går baklänges)
                    deltas.insert(0, current_deltas)

                # --- STEG 3: UPPDATERA VIKTER (Optimizer) ---
                for i, layer in enumerate(self.layers):
                    inputs_to_layer = outputs_by_layer[i]
                    for j, neuron in enumerate(layer):
                        delta = deltas[i][j]
                        # Uppdatera vikter
                        for k, input_val in enumerate(inputs_to_layer):
                            gradient = delta * input_val
                            neuron.weights[k] += learning_rate * gradient
                        # Uppdatera bias
                        neuron.bias += learning_rate * delta

            # Logga felet ibland
            if (epoch % 1000) == 0:
                # En enkel beräkning av Mean Squared Error bara för att se att det sjunker
                total_error = 0
                for x, y in zip(training_examples, training_solutions):
                    pred = self.predict(x)
                    total_error += sum((t - p) ** 2 for t, p in zip(y, pred))
                print(f"Epoch {epoch}, Error: {total_error:.4f}")

Lös XOR – Ett Problem för ett Nätverk

# --- Träningsdata för XOR ---


X_train = [[0, 0], [0, 1], [1, 0], [1, 1]]
y_train = [[0], [1], [1], [0]]

nn = NeuralNetwork(layer_sizes=[2, 2, 1])

print("Startar träning av neuralt nätverk för XOR...")
nn.fit(X_train, y_train, epochs=10000, learning_rate=0.1)
print("Träning klar!")

print("\nTestresultat:")
for inputs, solution in zip(X_train, y_train):
    prediction = nn.predict(inputs)
    print(f"Input: {inputs} -> Gissning: {prediction[0]:.4f}, Rätt svar: {solution[0]}")

När koden körs ser vi hur medelfelet stadigt minskar, ett bevis på att nätverket lär sig. Slutresultatet visar gissningar som är mycket nära de korrekta svaren (0 eller 1), vilket demonstrerar att nätverket har lyckats lära sig den icke-linjära relationen i XOR-data – en bedrift som krävde samverkan mellan flera neuroner och den sofistikerade träningsprocessen med Gradient Descent och Backpropagation.

Träningskomponenterna: En Djupdykning

För att bygga ett modernt nätverk räcker det inte med bara "Gradient Descent". Vi behöver välja rätt verktyg för varje del av processen.

1. Förlustfunktioner (Loss Functions)

Hur mäter vi "hur fel" nätverket har?

MSE (Mean Squared Error): Används för Regression (t.ex. huspriser). Straffar stora fel hårt.
Cross-Entropy Loss (Log Loss): Används för Klassificering (t.ex. Katt vs Hund). Mäter hur väl den förutsagda sannolikhetsfördelningen matchar verkligheten.

2. Optimerare (Optimizers)

Gradient Descent är som att gå nerför ett berg med ögonbindel. Men det finns smartare sätt att gå.

SGD (Stochastic Gradient Descent): Tar snabba, skakiga steg baserat på en liten del av datan åt gången.
Adam (Adaptive Moment Estimation): Den moderna standarden. Tänk dig en tung boll som rullar nerför berget. Den har momentum (fart) och anpassar sin hastighet för varje parameter individuellt. Den bromsar in i skarpa kurvor och gasar på raksträckor.

3. Aktiveringsfunktioner

Vi nämnde Sigmoid, men den har problem (den "dödar" gradienten för mycket stora/små tal).

ReLU (Rectified Linear Unit): f(x) = max(0, x). Enkel, snabb och löser många matematiska problem. Idag standard i de flesta dolda lager.
Softmax: Används i sista lagret för klassificering. Den tvingar alla outputs att summera till 1.0 (100%), vilket ger oss en snygg sannolikhetsfördelning.

4. Att Stoppa Överträning (Regularization)

Ett nätverk kan bli för bra på att memorera träningsdatan, så att det misslyckas på ny data (Överträning/Overfitting). Vi måste göra det svårare för nätverket att fuska.

Dropout: Under träning stänger vi slumpmässigt av t.ex. 50% av neuronerna i varje steg. Nätverket tvingas bli robust och inte lita för mycket på någon enskild neuron ("The Brain Damage analogy").
Early Stopping: Vi övervakar felet på en separat valideringsmängd. När felet börjar öka där (trots att det minskar på träningsdatan), avbryter vi träningen direkt.

5. Att tala nätverkets språk: One-Hot Encoding

Innan vi tittar på koden för hela nätverket måste vi lösa ett sista problem. Vår Perceptron svarade antingen 0 eller 1. Men om vi ska klassificera handskrivna siffror (0-9) har vi 10 möjliga svar. Hur får vi ett nätverk att svara "7"?

Ett neuralt nätverk svarar inte med en siffra. Det svarar med en sannolikhetslista. Om vi har 10 möjliga siffror, har vi 10 neuroner i vårt output-lager. Varje neuron representerar en siffra.

Om nätverket tror att bilden föreställer en femma, vill vi att neuron nummer 5 ska lysa starkt (vara nära 1.0) och alla andra ska vara släckta (nära 0.0).

Detta innebär att vi måste översätta vårt "facit". Vi kan inte träna nätverket genom att säga "Svaret är 5". Vi måste säga "Svaret är [0, 0, 0, 0, 0, 1, 0, 0, 0, 0]".

Detta kallas One-Hot Encoding.

Siffran 0 $\rightarrow$ [1, 0, 0, 0, 0, 0, 0, 0, 0, 0]
Siffran 1 $\rightarrow$ [0, 1, 0, 0, 0, 0, 0, 0, 0, 0]
...
Siffran 5 $\rightarrow$ [0, 0, 0, 0, 0, 1, 0, 0, 0, 0]

När vi tränar nätverket jämför vi output-lagrets lista (gissningen) med one-hot-listan (facit) för att beräkna felet.

De Två Stora Familjerna av ML

Klassisk maskininlärning delas oftast in i två huvudkategorier, baserat på vilken typ av data man har och vad man vill uppnå.

Supervised Learning (Övervakad Inlärning)

Detta är den vanligaste formen av maskininlärning. "Övervakad" betyder att vi tränar modellen på ett dataset där vi redan känner till de korrekta svaren. Vi har en "facitlista". Målet är att modellen ska lära sig den underliggande funktionen som kopplar ihop en input med en korrekt output, så att den sedan kan göra korrekta förutsägelser på ny, osedd data.

Inom övervakad inlärning finns två huvudtyper av problem:

Klassificering: Målet är att förutsäga en kategorisk etikett. Du sorterar data i fack.
- Exempel: Spam-filtrering. Modellen matas med tusentals e-postmeddelanden som manuellt har märkts som antingen "spam" eller "inte spam". Modellen lär sig att känna igen mönster (vissa ord, avsändare, länkar) som är typiska för skräppost. När ett nytt, okänt mejl kommer in, kan modellen klassificera det korrekt.
- Exempel: Bildigenkänning. Modellen tränas på miljontals bilder som är märkta med vad de föreställer ("katt", "hund", "bil"). Den lär sig känna igen visuella mönster av pixlar som utgör en katt, och kan sedan identifiera katter i helt nya bilder.
Regression: Målet är att förutsäga ett kontinuerligt, numeriskt värde.
- Exempel: Huspriser. Modellen matas med data om tusentals sålda hus, där varje hus har egenskaper (input: antal rum, yta, läge) och ett känt slutpris (output). Modellen lär sig hur dessa egenskaper viktas för att förutsäga priset på ett nytt hus som kommer ut på marknaden.
- Exempel: Försäljningsprognoser. Ett företag matar en modell med historisk försäljningsdata, information om väder, helgdagar och reklamkampanjer. Modellen lär sig sambanden och kan sedan förutsäga hur mycket glass de kommer att sälja nästa vecka.

Supervised learning - efter granskning av korrekta svar kan AI själv producera korrekta svar

En fundamental princip inom övervakad inlärning är uppdelningen i tränings- och testdata. Man tränar alltid modellen på en del av datan (t.ex. 80%) och utvärderar sedan dess prestanda på en separat, "osedd" del (de återstående 20%). Att testa på samma data som man tränat på vore som att ge en student exakt samma frågor på provet som de haft på sina övningsuppgifter – det mäter bara förmågan att memorera, inte att generalisera och faktiskt "kunna" ämnet.

Tumregel: Memorera vs. Generalisera

Målet med all maskininlärning är generalisering, inte memorering. En bra modell är inte en som kan rabbla upp exakta svar från träningsdatan, utan en som har lärt sig de underliggande mönstren så väl att den kan göra korrekta förutsägelser på helt ny och osedd data.

Fallstudie 1: Linjär Regression

Detta är ett av de enklaste exemplen på regression. Målet är att dra en rak linje som bäst passar en samling datapunkter, t.ex. för att förutsäga huspriser baserat på boyta.

Modellen: En enkel linje, y = mx + c, där m (lutning) och c (skärningspunkt) är modellens "vikter".
Kostnadsfunktionen: Man använder Mean Squared Error (MSE), som beräknar det genomsnittliga kvadratiska avståndet från varje datapunkt till linjen. Målet är att hitta den linje som minimerar detta totala avstånd.
Lärandet: Modellen använder Gradient Descent för att hitta de optimala värdena på m och c. Den startar med en slumpmässig linje, beräknar felet (MSE), och justerar sedan m och c stegvis i den riktning som minskar felet, tills linjen passar datan så bra som möjligt.

Python-exempel

Med biblioteket scikit-learn kan man träna en linjär regressionsmodell på bara några rader kod:

from sklearn.linear_model import LinearRegression

# Ladda din data (X = boyta, y = pris)
model = LinearRegression()
model.fit(X, y)
# Modellen är nu tränad och kan göra förutsägelser

Fallstudie 2: Beslutsträd i Praktiken

Ett beslutsträd är en kraftfull och lättolkad modell för klassificering. Den lär sig en serie av OM-DÅ-regler som delar upp datan i allt renare grupper. Istället för att bara beskriva det, låt oss bygga ett och visualisera det med scikit-learn på vårt välkända Iris-dataset.

Hur det fungerar: Algoritmen försöker hitta den bästa frågan att ställa för att dela upp datan. Vad är en "bra" fråga? Det är en fråga (t.ex. "Är petal length < 2.45 cm?") som resulterar i två grupper som är så "rena" som möjligt, dvs. där varje grupp så långt som möjligt bara innehåller en enda klass. För att mäta detta används ett mått som Gini Impurity. Processen upprepas sedan för varje ny grupp, och trädet växer tills det har klassificerat all data.

Det bästa sättet att förstå ett beslutsträd är att se det. Koden nedan tränar en DecisionTreeClassifier och använder sedan matplotlib för att rita upp exakt de regler som modellen har lärt sig.

# decision_tree_iris.py
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier, plot_tree

# 1. Ladda data
iris = load_iris()
X, y = iris.data, iris.target

# 2. Skapa och träna modellen
# Vi sätter max_depth=3 för att trädet inte ska bli för stort och svårläst
clf = DecisionTreeClassifier(max_depth=3, random_state=42)
clf.fit(X, y)

# 3. Visualisera trädet
plt.figure(figsize=(20,10))
plot_tree(clf,
          filled=True,
          rounded=True,
          class_names=iris.target_names,
          feature_names=iris.feature_names)
plt.title("Beslutsträd tränat på Iris-datasetet")
plt.show()

När du kör koden kommer ett diagram att visas. Varje ruta (nod) i trädet representerar en fråga. Genom att följa frågorna från roten (översta noden) ner till ett löv (en nod utan barn) kan du se exakt hur modellen skulle klassificera en ny blomma. Detta är en av de största fördelarna med beslutsträd: till skillnad från ett neuralt nätverk är de inte en "svart låda". Vi kan inspektera och förstå exakt hur de resonerar.

Bortom Enskilda Träd: Ensemble-metoder

Ett enda beslutsträd kan vara instabilt. Om du ändrar en liten detalj i träningsdatan kan hela trädet se annorlunda ut. Lösningen? Bygg en skog! Detta kallas Ensemble Learning – att kombinera många svaga modeller för att skapa en stark.

Random Forest (Slumpmässig Skog): Tänk dig att du tränar 100 beslutsträd. Varje träd får bara se en slumpmässig del av datan och får bara använda en slumpmässig del av frågorna (features). När vi ska klassificera en ny datapunkt får alla 100 träd rösta. Majoriteten vinner. Detta minskar risken för fel drastiskt (Bagging).

from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split

# Ladda dataset
data = load_wine()
X_train, X_test, y_train, y_test = train_test_split(data.data, data.target, test_size=0.3)

# Träna en slumpmässig skog
clf = RandomForestClassifier(n_estimators=100) # 100 träd
clf.fit(X_train, y_train)

print(f"Noggrannhet: {clf.score(X_test, y_test):.2f}")

Boosting (XGBoost, CatBoost, LightGBM): Här tränar vi inte träden parallellt, utan i serie.
- Träd 1 gör sina gissningar. Vissa blir fel.
- Träd 2 tränas specifikt för att rätta till Träd 1:s misstag.
- Träd 3 tränas för att rätta till Träd 2:s misstag. Detta skapar en extremt skarp modell. XGBoost och CatBoost är idag dominerande i tävlingar på Kaggle när det gäller strukturerad data (tabeller), ofta överlägsna neurala nätverk.

Support Vector Machines (SVM) & The Kernel Trick

Innan djupinlärning tog över var SVM kungen av klassificering. Idén är geometrisk: Hitta den "bredaste gatan" (margin) som separerar två klasser av data.

Men vad om datan inte kan separeras med en rak linje (som i XOR-problemet)? SVM har ett matematiskt ess i rockärmen: The Kernel Trick. Föreställ dig att du har röda och blå punkter på ett papper som inte kan separeras med en linje. Kernel-tricket är som att lyfta upp pappret i 3D och vika det, så att de röda punkterna hamnar på ena sidan av veckat och de blå på andra. Genom att projicera data i högre dimensioner blir omöjliga problem plötsligt lösbara med en enkel "rak linje" (hyperplan) i den nya dimensionen.

import matplotlib.pyplot as plt
from sklearn.datasets import make_circles
from sklearn.svm import SVC
import numpy as np

# 1. Skapa "omöjlig" data (cirklar inuti cirklar)
X, y = make_circles(n_samples=100, factor=0.1, noise=0.1)

# 2. Träna en SVM med 'RBF' kernel (Radial Basis Function)
# Detta är "tricket" som lyfter datan till oändliga dimensioner
clf = SVC(kernel='rbf', C=1.0)jo men 2,2,1
clf.fit(X, y)

# 3. Visualisera beslutsgränsen
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='coolwarm')

# Skapa ett rutnät för att rita bakgrundsfärgen
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
xx, yy = np.meshgrid(np.linspace(xlim[0], xlim[1], 30),
                     np.linspace(ylim[0], ylim[1], 30))
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

# Rita konturerna (gränsen)
ax.contour(xx, yy, Z, colors='k', levels=[0], alpha=0.5, linestyles=['-'])
plt.title("SVM med Kernel Trick: Cirklar lösta!")
plt.show()

Att Mäta Framgång: Bortom "Accuracy"

Hur vet vi om vår modell är bra? Det intuitiva måttet är Accuracy (Andel korrekta svar). Men det kan vara livsfarligt missvisande.

Exempel: Cancerdiagnos Antag att du bygger en AI för att hitta en ovanlig cancer som bara 1% av befolkningen har. Din modell är lat och gissar alltid: "Frisk".

Accuracy: 99% (Fantastiskt!)
Nytta: 0% (Den hittar ingen cancer alls).

För att hantera detta (obalanserad data) använder vi bättre mått:

Precision: Av alla fall modellen kallade cancer, hur många var cancer? (Undvik falskt alarm).
Recall (Sensitivitet): Av alla som faktiskt hade cancer, hur många hittade modellen? (Missa inga fall).
F1-Score: Ett balanserat medelvärde av Precision och Recall.

I cancerexemplet hade vår lata modell haft Recall = 0%, vilket direkt hade avslöjat den som värdelös.

from sklearn.metrics import classification_report, confusion_matrix

# Låt oss se hur vår Random Forest presterade i detalj
y_pred = clf.predict(X_test)

print("Confusion Matrix:")
print(confusion_matrix(y_test, y_pred))

print("\nClassification Report:")
print(classification_report(y_test, y_pred, target_names=data.target_names))

Unsupervised Learning (Oövervakad Inlärning)

Här har vi den motsatta och ofta mer utmanande situationen. Vi har ett dataset, men vi har ingen aning om vad de "korrekta" svaren är. Vi har ingen facitlista eller fördefinierade etiketter. Målet är istället att låta modellen agera som en digital upptäcktsresande och på egen hand hitta dolda mönster, strukturer och samband i datan. Det handlar inte om att förutsäga ett känt svar, utan om att skapa förståelse ur kaos.

De två vanligaste uppgifterna inom oövervakad inlärning är clustering och dimensionsreducering, och båda löser fundamentala problem när man arbetar med stora datamängder.

1. Clustering (Klustring)

Clustering-algoritmer har som mål att hitta den dolda, naturliga grupperingen i datan. Modellen försöker placera datapunkter som liknar varandra i "kluster" och samtidigt se till att klustren är så olika varandra som möjligt.

Exempel: Kundsegmentering. En butikskedja matar in anonymiserad köpdata från tusentals kunder (vad de köper, när de handlar, hur mycket de spenderar). Clustering-algoritmen kanske på egen hand identifierar tre distinkta grupper: "studenter som handlar billigt på kvällar", "barnfamiljer som storhandlar på helger" och "pensionärer som köper specifika varor på förmiddagar".

Varför är detta viktigt? Att bara ha en stor mängd kunddata är inte särskilt användbart. Clustering omvandlar denna rådata till värdefull insikt.

Målinriktad marknadsföring: Istället för att skicka samma reklam till alla, kan företaget nu skicka specifika erbjudanden som är relevanta för varje grupp. Detta ökar försäljningen och kundnöjdheten.
Upptäcka nya marknader: Kanske hittar algoritmen ett oväntat kluster, t.ex. "personer som bara köper ekologiska produkter sent på tisdagar". Detta kan vara en helt ny nisch att utforska.
Anomalidetektering: Om en ny datapunkt inte passar in i något av de befintliga klustren kan det vara en avvikelse, t.ex. ett bedrägligt köpbeteende eller ett fel i systemet.

2. Dimensionality Reduction (Dimensionsreducering)

Modern data innehåller ofta hundratals eller tusentals variabler (dimensioner) för varje datapunkt. Tänk dig en patientjournal med data om allt från blodtryck och vikt till hundratals olika genuttryck. Detta skapar två stora problem: det blir omöjligt för en människa att visualisera, och det kan göra maskininlärningsmodeller extremt långsamma och ineffektiva (ett fenomen som kallas "The Curse of Dimensionality").

Dimensionsreducering är en samling tekniker för att på ett intelligent sätt "komprimera" datan. Målet är att koka ner de hundratals variablerna till ett fåtal nya, super-variabler som fortfarande behåller den viktigaste informationen. Det är som att skriva en sammanfattning av en bok – du behåller kärnan i handlingen men tar bort onödiga detaljer.

Varför är detta viktigt? Detta är inte bara en teoretisk städövning, utan en kritisk process för att göra maskininlärning praktiskt genomförbar.

Snabbare träning: En modell som tränar på 10 "super-variabler" istället för 1000 originalvariabler kan bli klar på minuter istället för dagar, vilket sparar enorma mängder tid och beräkningskraft.
Minskat brus: Många av de ursprungliga variablerna kan vara redundanta (t.ex. ha både längd i meter och i fot) eller bara vara "brus". Dimensionsreducering hjälper till att filtrera bort detta och fokusera på den verkliga underliggande signalen, vilket ofta leder till mer träffsäkra modeller.
Visualisering: Genom att reducera dimensionerna till 2 eller 3 kan vi faktiskt plotta datan i en graf och visuellt inspektera den. Detta är ett oerhört kraftfullt verktyg för att förstå datans struktur och se om det finns tydliga kluster innan man ens börjar träna en mer komplex modell.

Dimensionsreduceringens Kung: PCA (Principal Component Analysis)

Om du tävlar i AI (t.ex. IOAI) kommer du ständigt stöta på data med för många kolumner. Det klassiska verktyget för att hantera detta är PCA.

Tänk dig ett moln av punkter format som en utdragen baguette i 3D-rymden.

PCA hittar "Huvudriktningen": Den drar en linje genom baguettens längd (där datan varierar mest). Detta är "Principal Component 1".
PCA hittar nästa riktning: Den drar en ny linje vinkelrätt mot den första, genom baguettens bredd. Detta är "Principal Component 2".
Platta till: Genom att bara behålla dessa två linjer och kasta bort höjden (som kanske bara är smulor/brus), har vi komprimerat 3D-objektet till en 2D-skiva utan att tappa den viktiga formen.

I tävlingar används PCA ofta för att:

Visualisera komplex data i 2D.
Ta bort brus (behåll bara de viktigaste komponenterna).
Skapa nya features som är bättre för din modell.

Unsupervised learning - AI hittar själv mönster/likheter i datat och använder detta för att dra slutsatser

Fallstudie: K-Means Clustering i Praktiken

Detta är den mest kända clustering-algoritmen. Målet är att dela in datan i K antal fördefinierade kluster. Algoritmen fungerar iterativt:

Den startar med K slumpmässiga mittpunkter (centroider).
Den tilldelar varje datapunkt till den närmaste centroiden.
Den räknar om positionen för varje centroid baserat på medelvärdet av alla punkter som nu tillhör den.
Den upprepar steg 2 och 3 tills centroiderna slutar flytta på sig.

Låt oss se detta i praktiken. Koden nedan skapar först slumpmässig "blob"-data (som ser ut som moln av punkter) och använder sedan KMeans från scikit-learn för att hitta de underliggande grupperna.

# kmeans_visualization.py
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans

# 1. Skapa ett syntetiskt dataset
# Vi skapar 300 punkter fördelade runt 4 olika centrum.
X, y_true = make_blobs(n_samples=300, centers=4,
                       cluster_std=0.70, random_state=0)

# 2. Skapa och träna K-Means modellen
# Vi talar om för modellen att vi letar efter 4 kluster.
kmeans = KMeans(n_clusters=4, random_state=0, n_init=10)
kmeans.fit(X)
y_kmeans = kmeans.predict(X)

# 3. Visualisera resultatet
plt.figure(figsize=(8, 6))
# Rita upp punkterna, färgade efter det kluster de tilldelats av KMeans
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis')

# Rita ut de slutgiltiga centroiderna som modellen hittat
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.75, marker='X')
plt.title("K-Means Clustering i Aktion")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.show()

Resultatet är en tydlig visualisering av oövervakad inlärning. Vi gav aldrig modellen något facit (y_true används inte i träningen), men den lyckades ändå på egen hand identifiera de fyra distinkta grupperna i datan och hitta deras mittpunkter. Detta är kärnan i clustering: att hitta struktur i data utan förkunskap.

Fler Verktyg i Lådan

K-Means är inte ensam. Beroende på datans form behövs olika verktyg:

1. KNN (K-Nearest Neighbors) "Säg mig vilka dina vänner är, så ska jag säga vem du är." KNN är en enkel men kraftfull algoritm som klassificerar en ny datapunkt genom att titta på dess grannar.

from sklearn.neighbors import KNeighborsClassifier
# ... (Ladda data som i tidigare exempel) ...
# K=3 betyder "Titta på de 3 närmaste grannarna och låt dem rösta"
neigh = KNeighborsClassifier(n_neighbors=3)
neigh.fit(X, y)
# Enkelt, men kan bli långsamt med enorma dataset eftersom den måste mäta avstånd till ALLA punkter.

2. Gaussian Mixture Models (GMM) K-Means antar att alla kluster är perfekta, runda cirklar. Men verkligheten är ofta "utdragen". GMM är smartare; den antar att kluster är ovala (Gaussiska fördelningar).

from sklearn.mixture import GaussianMixture

# GMM hittar inte bara mitten, utan också formen (variansen) på klustret
gmm = GaussianMixture(n_components=4)
gmm.fit(X)
labels = gmm.predict(X)
# GMM ger också sannolikheter: "55% chans att du tillhör Kluster A"
probs = gmm.predict_proba(X)

3. Autoencoders Ett neuralt nätverk som lär sig att komprimera data. (Vi kommer att bygga en komplett Autoencoder för bildrestaurering i Kapitel 8, så håll ut!)

Hantverket: Från Rådata till Modell

Att känna till algoritmerna är en sak. Att få dem att fungera i verkligheten är en annan. En Data Scientist lägger ofta 80% av sin tid på datapreparering och bara 20% på själva modelleringen.

1. Hantera det som saknas (NaNs)

Verklig data är smutsig. Värden saknas (NaN - Not a Number).

Drop: Kasta bort rader som saknar data? (Risk att tappa information).
Impute: Gissa värdet? (T.ex. fyll i med medelvärdet av alla andra rader).

2. Feature Extraction & Engineering

Datorer förstår bara siffror. Hur matar man in en text eller en bild?

Bilder: Varje pixel blir en siffra (0-255).
Text: Vi använder "Word Embeddings" (som Word2Vec) för att omvandla ord till vektorer av siffror.
Engineering: Att skapa nya, smartare variabler. T.ex. istället för att mata in "Datum", skapa variabeln "Är det helg?" som kanske är mer relevant för försäljning.

3. Skalning av data (Normalization)

Ett vanligt misstag är att mata in rådata där olika inputs har helt olika skalor, t.ex. Ålder (0–100) och Lön (0–50 000).

Varför ska vi normalisera? För det första handlar det om att göra det möjligt för algoritmen att hitta rätt vikter. Om du matar in jättestora tal (som 50 000) måste nätverket hitta en extremt liten vikt för att balansera kalkylen. Risken är stor att vår learning rate (storleken på stegen vi tar när vi tränar) är större än den precision som krävs för att hitta den där mikroskopiska vikten. Vi kliver helt enkelt över lösningen gång på gång.

Men det finns en teknisk fördel till. En del aktiveringsfunktioner (som Sigmoid och ReLU) är designade för att arbeta inom specifika intervall.

Sigmoid: Om input-värdet är stort "mättas" funktionen (blir platt), derivatan blir noll och nätverket slutar lära sig.
ReLU: Om värdena är för stora kan beräkningarna explodera längre in i nätverket.

Genom att normalisera datan till ett standardintervall (t.ex. 0 till 1) placerar vi datan i ett intervall där dessa matematiska funktioner presterar som bäst.

Win-win Det fina är att detta är en linjär transformation. Vi ändrar skalan på axlarna, men den inbördes relationen mellan datapunkterna är exakt densamma. En hög lön är fortfarande högre än en låg lön, med exakt samma proportioner. Vi får alltså en matematiskt optimerad träningsmiljö utan att förvanska informationen i vårt data.

Hur gör man? Vi måste skala om datan så att alla inputs "spelar på samma planhalva". Det finns två huvudmetoder (du kommer se exempel på detta i övningsuppgiften om pingviner):

Min-Max Normalization: Skalar om datan så att alla värden tvingas in mellan 0 och 1.
- Formel: (värde - min) / (max - min)
Standardization (Z-score): Centrerar datan runt 0. Medelvärdet blir 0 och standardavvikelsen 1. Detta är ofta bättre om datan innehåller extrema utliggare (outliers).
- Formel: (värde - medelvärde) / standardavvikelse

När ska man göra det? I princip alltid när du använder Neurala Nätverk (för att hjälpa Gradient Descent) eller algoritmer som baseras på geometriska avstånd som K-Means, KNN och SVM. Det är mindre kritiskt för träd-baserade modeller (som Decision Trees och Random Forest) eftersom de tittar på varje variabel isolerat.

4. Validering: Cross-Validation

Att bara dela upp data i Train/Test en gång kan vara riskabelt (du kanske hade tur/otur med uppdelningen). K-Fold Cross-Validation: Dela datan i 5 delar. Träna på 4, testa på 1. Rotera och upprepa 5 gånger. Medelvärdet ger en mycket mer sann bild av modellens kvalitet.

5. Hyperparameter Tuning

Hur vet man om learning_rate ska vara 0.1 eller 0.01? Om Random Forest ska ha 10 träd eller 100? Dessa inställningar kallas hyperparametrar.

Grid Search: Testa systematiskt alla kombinationer (långsamt men noggrant).
Random Search: Testa slumpmässiga kombinationer (ofta förvånansvärt effektivt).

6. Tävlingstips: Hur man vinner en AI-olympiad

Om du tittar på uppgifterna i IOAI eller på Kaggle, räcker det sällan med att bara "köra en modell". Här är hemligheterna som vinnarna använder:

Feature Engineering är Kung: Modellen är bara så smart som datan du ger den.
- Kombinera: Har du "Längd" och "Bredd"? Skapa "Area".
- Interaktioner: Multiplicera variabler med varandra.
- Domänkunskap: I Titanic-exemplet: "Antal syskon" + "Antal föräldrar" = "Familjestorlek". En ensam resenär beter sig annorlunda än en stor familj.
Ensembling & Stacking: Varför lita på en modell när du kan lita på tio?
- Träna en Random Forest, en XGBoost och en SVM.
- Låt dem rösta (Average) eller träna en ny modell (Meta-learner) som tar de andras gissningar som input för att göra slutgiltiga beslutet. Detta kallas Stacking.

Proffsens Verktygslåda

När du lämnar lekstugan och börjar jobba på riktigt kommer du stöta på dessa namn ständigt:

Pandas: Python-biblioteket för att hantera tabell-data ("Excel på steroider"). Oumbärligt för att städa data och hantera NaNs.
Seaborn: Bygger på Matplotlib men gör det mycket enklare att rita snygga, statistiska grafer.
Kaggle: Världens största community för Data Science. Här hittar du dataset, tävlingar och miljontals rader exempelkod.
Hugging Face: "GitHub för AI". Platsen där alla moderna modeller (speciellt Transformers) delas och laddas ner ifrån.

Svenska exempel

Under 2000-talet, när datorkraften och mängden tillgänglig data exploderade, blev maskininlärning ryggraden i många av de mest framgångsrika tech-bolagen.

Klarna: Hela Klarnas affärsmodell bygger på att snabbt kunna fatta ett kreditbeslut. När du klickar på "Köp nu, betala senare" måste de på en bråkdels sekund avgöra hur troligt det är att du faktiskt kommer att betala. Detta görs med en regressionsmodell som tar hundratals variabler (din köphistorik, tid på dygnet, typ av produkt, etc.) och producerar en "riskpoäng". Detta är klassisk maskininlärning i ett nötskal, där AI inte bara är en teknisk finess, utan en direkt förutsättning för hela affären.
Spotify: Hur kan Spotify upplevas som att den "känner" din musiksmak? Deras rekommendationsmotorer är ett sofistikerat exempel på hur flera ML-tekniker samverkar.
- Kollaborativ filtrering (Unsupervised): Systemet använder clustering för att hitta andra användare vars musiksmak liknar din. Den tittar sedan på vilka låtar de lyssnar på, som du ännu inte har upptäckt, och rekommenderar dem till dig. Den antar att om personer med liknande historisk smak gillar en viss låt, är chansen stor att du också kommer att göra det.
- Content-Based Filtering (Supervised): Spotify analyserar även ljudfilerna direkt för att extrahera hundratals musikaliska egenskaper (tempo, akustiskhet, "dansbarhet", tonart etc.). När du lyssnar mycket på en viss typ av låt, tränas en klassificeringsmodell att förstå din "smakprofil". Den kan sedan hitta helt nya låtar från okända artister som har liknande musikaliska egenskaper och rekommendera dem till dig.

TODO

Verifiera dessa studier med tech-bloggarna som beskriver användningen.

Perspektiv på Klassisk Maskininlärning

Det filosofiska perspektivet: Empirismens Återkomst

Maskininlärning representerar en seger för empirismen. AI-forskare slutade försöka förprogrammera "sanningen". Istället skapade de system som kunde lära sig från erfarenhet (data). En ML-modell är en modern "Tabula Rasa", en oskriven tavla som fylls med kunskap genom observation av världen. Detta skifte från logik till statistik är det enskilt viktigaste som hänt i AI:s historia.

Det ekonomiska perspektivet: Från Akademisk Teori till Affärskritisk Motor

Den kanske största anledningen till att maskininlärning exploderade var att den skapade ett enormt och mätbart ekonomiskt värde. För första gången kunde företag gå från att reagera på vad deras kunder hade gjort, till att med hög precision förutsäga vad de skulle komma att göra. Amazons rekommendationsmotor, som föreslår produkter baserat på vad liknande kunder har köpt, är ett klassiskt exempel. Denna funktion, driven av maskininlärning, sägs stå för över en tredjedel av deras totala försäljning. ML var inte längre en akademisk leksak; det var en affärskritisk motor som kunde omvandla data till miljarder.

Det sociologiska perspektivet: Filterbubblor och Polarisering

När företag som YouTube och Facebook (numera Meta) började använda maskininlärning för att personalisera sina flöden, uppstod en oavsiktlig men kraftfull bieffekt. Genom att ständigt visa oss innehåll som liknar det vi redan gillat, skapade algoritmerna det som aktivisten Eli Pariser kallade filterbubblor.

Den osynliga handen

Algoritmerna har inget ont uppsåt. Deras enda mål är att maximera din tid på plattformen. Men genom att optimera för engagemang, råkar de oavsiktligt gynna innehåll som är chockerande, upprörande eller extremt. Detta är en oavsiktlig konsekvens av ett system som är designat för att fånga din uppmärksamhet, inte för att ge dig en balanserad bild av världen.

Ditt personliga informationsuniversum skulpteras av algoritmer för att passa just dina preferenser. Problemet är att du inte ser vad som filtreras bort. Detta förstärks av algoritmisk amplifiering: innehåll som väcker starka känslor (ilska, rädsla, glädje) genererar mer engagemang (klick, kommentarer, delningar) och blir därför automatiskt prioriterat av systemet. Resultatet är att mer extrema eller polariserande budskap ofta får större spridning. Över tid kan detta leda till att vi hamnar i eko-kammare, där våra egna åsikter ständigt upprepas och förstärks, och vi får en förvrängd bild av hur "den andra sidan" tänker. Detta har pekats ut som en starkt bidragande orsak till den ökande politiska polariseringen i många länder. Detta går även att utnyttja för att uppnå specifika ändamål. Det mest ökända exemplet är Cambridge Analytica-skandalen, där ML-driven mikrotargeting användes för att försöka påverka valutgången i USA 2016.

Mikrotargeting

Mikrotargeting är användningen av onlinedata för att skräddarsy reklambudskap till individer, baserat på identifiering av mottagarnas personliga sårbarheter.

Det kognitiva & psykologiska perspektivet: Uppmärksamhetsekonomin och den Algoritmiska Blicken

Varför är dessa personaliserade flöden så beroendeframkallande? Svaret ligger i hur de är designade för att utnyttja vårt belöningssystem. I en värld av informationsöverflöd är den verkliga bristvaran mänsklig uppmärksamhet. Hela affärsmodellen för många sociala medier bygger på att fånga och behålla din uppmärksamhet så länge som möjligt, för att kunna visa dig så många annonser som möjligt.

För att göra detta använder de en psykologisk mekanism som kallas intermittent förstärkning. Det är samma princip som gör spelautomater så beroendeframkallande. Du vet aldrig när nästa belöning (en rolig video, en intressant nyhet, en like på din bild) kommer att dyka upp. Denna oförutsägbarhet gör att din hjärna fortsätter att utsöndra dopamin, vilket får dig att fortsätta skrolla.

Över tid kan detta leda till att vi utvecklar en "algoritmiskt synsätt", där vi omedvetet börjar anpassa vårt eget beteende för att maximera den belöning vi får från plattformen. Vi börjar posta bilder, skriva inlägg eller skapa videor som vi tror att algoritmen kommer att gilla, snarare än vad som är mest autentiskt för oss själva. Vi börjar se på vår egen verklighet genom linsen av "kommer detta att fungera online?". Tänk på detta om ni någonsin tycker att influencer livsstilen känns lockande.

Övningar

Machine Learning

I detta kapitel går vi från den teoretiska förståelsen av neuroner och nätverk till att experimentera med dem. Läroboken har redan visat dig hur man bygger dessa modeller från grunden och hur man använder professionella verktyg. I dessa övningar kommer du att ta den koden, modifiera den, och testa dess gränser för att bygga en djupare, praktisk intuition.

Verktyg: Visual Studio Code med en Python-installation och nödvändiga bibliotek (numpy, scikit-learn, matplotlib, seaborn).

Övning 0: Bevisa Perceptronens Gränser

Syfte: Att praktiskt demonstrera varför en enskild Perceptron inte kan lösa icke-linjära problem som XOR, precis som Minsky och Papert argumenterade.

Skapa en fil: test_perceptron_limits.py.
Använd Perceptron-klassen: Importera eller klistra in Perceptron-klassen från läroboken (den som har en fit-metod).

Skapa XOR-data:

import numpy as np

# Data för en XOR-grind
X_train = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y_train = np.array([0, 1, 1, 0])

Träna och Testa: Använd samma träningsloop som i textbokens "fest-scenario"-exempel, men med din XOR-data. Träna i ett stort antal epoker (t.ex. 500).

# Skapa och träna din Perceptron
p = Perceptron(num_inputs=2, n_iterations=500)
p.fit(X_train, y_train)

# Testa den tränade modellen
print("\nTestar den tränade Perceptronen på XOR-data:")
for input, target in zip(X_train, y_train):
    prediction = p.predict(input)
    print(f"Input: {input}, Prediktion: {prediction}, Korrekt: {target}")

Analysera: Kör skriptet. Kommer din Perceptron någonsin att lära sig att lösa XOR-problemet korrekt för alla fyra fallen? Vad händer med vikterna och biasen under träningens gång?

Reflektera

Du har nu praktiskt bevisat Perceptronens begränsning. Den kan inte hitta en rak linje som separerar XOR-datan. Detta motiverar varför vi behöver gå vidare till nästa nivå: nätverk av neuroner.

Övning 1: Överlevare från Titanic

Syfte: Din perceptron beräknar en matematisk formel. Den kraschar om du matar in text ("male") eller tomma värden (NaN). Här får du öva på rollen som Data Engineer: att städa och forma data så att en maskin kan förstå den. Verkligheten för många AI uppgifter är att detta kan vara en stor del av jobbet.

Målet är binärt, för en given passagerare, gissa om den överlevde (1) eller dog (0)?

Ladda och Inspektera:

import seaborn as sns
import pandas as pd

# Ladda datasetet
titanic = sns.load_dataset("titanic")

# Välj ut relevanta kolumner (Features)
# Survived är vårt FACIT (Target)
df = titanic[["survived", "pclass", "sex", "age", "fare"]]

print("--- Före städning ---")
print(df.head())
print(df.info()) # Notera att 'age' saknar många värden!

Data Cleaning (städning): Vi måste göra tre saker:

Hantera NaN: Vi kan inte gissa åldern på de som saknar den (just nu). Ta bort rader som saknar data.
Text till siffror: "male"/"female" måste bli 0/1.
Normalisering: age (0-80) och fare (0-500) har helt olika skalor. Vi måste klämma in dem mellan 0-1 så att inte biljettpriset "dränker" all annan info.

# 1. Ta bort rader med saknade värden
df = df.dropna()

# 2. Mappa text till siffror
# Vi gör om 'sex' så att male=0, female=1
df["sex"] = df["sex"].map({"male": 0, "female": 1})

# 3. Normalisera numeriska värden (Min-Max)
# Formel: (värde - min) / (max - min)
for col in ["age", "fare", "pclass"]:
    df[col] = (df[col] - df[col].min()) / (df[col].max() - df[col].min())

print("\n--- Efter städning ---")
print(df.head())

Träna din Perceptron:
- Skapa inputs (listor av pclass, sex, age, fare) och targets (listor av survived).
  
  Såhär skulle det kunna se ut:
```
# X = Allt utom 'survived'. .values gör om det till en NumPy-array (snabbare)
X = df[["pclass", "sex", "age", "fare"]].values

# y = Bara 'survived'
y = df["survived"].values
```
- Träna din Perceptron.
- Beräkna din accuracy genom att summera hur många gånger du får rätt och dela med antalet testfall du testar.

Övning 2: Pingvin-hjärnan (multi-class & one-hot)

Problemet: Titanic var enkelt: Ja eller Nej. Men tänk om vi vill veta vilken art en pingvin tillhör? Svaret är inte 0 eller 1, utan "Adelie", "Chinstrap" eller "Gentoo".

En ensam perceptron kan inte svara på detta. Vi behöver flera där vardera kan försöka identifiera respektive art. Vi ska bygga klassen PenguinNetwork som innehåller tre perceptroner:

En som är expert på att hitta Adelie.
En som är expert på att hitta Chinstrap.
En som är expert på att hitta Gentoo.

Nätverket kommer svara med en lista av identifierade arter. Svaret [1,0,0] betyder att nätverket har identifierat Adelie. Svaret [0,0,1] betyder Gentoo.

Steg 1: One-Hot encoding av facit

För att träna tre experter behöver vi konstruera vårt facit. Om en pingvin är Chinstrap, ska facit se ut så här: [0, 1, 0].

När facit ser ut så betyder det att:

Adelie-experten ska tränas mot 0.
Chinstrap-experten ska tränas mot 1.
Gentoo-experten ska tränas mot 0.

from per import Perceptron
import seaborn as sns
import numpy as np
import pandas as pd

penguins = sns.load_dataset("penguins").dropna()
X = penguins[["flipper_length_mm", "bill_length_mm"]].values
X = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0)) # Normalisering

# One-Hot Encoding av arterna
# pandas .get_dummies() gör detta automatiskt åt oss!
y_onehot = pd.get_dummies(penguins["species"],dtype=int).values

print(f"Exempel på one-hot facit: {y_onehot[0]}")
# T.ex: [1, 0, 0] (Betyder Adelie)

Steg 2: Bygg Pingvin-hjärnan

Fyll i koden för klassen nedan. Använd din existerande Perceptron (den som returnerar 1/0).

from perceptron import Perceptron
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

class PenguinNetwork:
    def __init__(self, n_inputs=2):
        self.perceptrons = [Perceptron(n_inputs), Perceptron(n_inputs), Perceptron(n_inputs)]
        self.species_names = ["Adelie", "Chinstrap", "Gentoo"]

    def train(self, inputs, one_hot_targets, cycles=1000):
        for i, p in enumerate(self.perceptrons):
            # Skapa en lista med facit BARA för denna art.
            # one_hot_targets[:, i] betyder: "Ta alla rader (:), men bara kolumn 'i'"
            specific_target = one_hot_targets[:, i]
            p.fit(inputs, specific_target, cycles)

    def predict(self, input_data):
        # Fråga alla tre perceptronerna
        return [p.predict(input_data) for p in self.perceptrons]

# --- Kör koden ---
brain = PenguinNetwork()
brain.train(X, y_onehot)

# Testa på en pingvin
# Testa på en pingvin
test_penguin = X[0]
svar = brain.predict(test_penguin)
svar_index = np.argmax(svar) # vilket index var högst
svar_pingvin = penguins["species"].unique()[svar_index] # vilken pingvin har detta index
print(f"Networks råa svar: {brain.predict(test_penguin)}")
print(f"Networks pingvin val: {svar_pingvin}")

Steg 3: Statistik

Lägg till följande i ditt PenguinNetwork:

def get_expert_accuracy(self, expert_index, inputs, one_hot_targets):
    """Kollar hur ofta en specifik expert har rätt (Binärt: Ja/Nej)."""
    expert = self.perceptrons[expert_index]
    correct = 0
    specific_targets = one_hot_targets[:, expert_index]

    for i, x in enumerate(inputs):
        # Om sannolikhet > 0.5 gissar den Ja (1), annars Nej (0)
        pred = 1 if expert.predict(x) > 0.5 else 0
        if pred == specific_targets[i]:
            correct += 1
    return (correct / len(inputs)) * 100

def get_overall_accuracy(self, inputs, one_hot_targets):
    """Kollar hur ofta Hjärnan väljer rätt vinnare."""
    correct = 0
    for i, x in enumerate(inputs):
        # Hitta vinnaren (index 0, 1 eller 2)
        probs = self.predict(x)
        winner_idx = np.argmax(probs)

        # Facit: Vilket index har en 1:a i one_hot_targets?
        true_idx = np.argmax(one_hot_targets[i])

        if winner_idx == true_idx:
            correct += 1
    return (correct / len(inputs)) * 100

Sedan kan du använda dessa metoder efter att du tränat din pingvin-hjärna på detta sätt:

print("\n--- Resultat ---")
# Skriv ut accuracy för varje expert
for i, name in enumerate(brain.species_names):
    acc = brain.get_expert_accuracy(i, X, y_onehot)
    print(f"Expert på {name}: {acc:.1f}% rätt (Binärt)")

# Skriv ut total accuracy
total_acc = brain.get_overall_accuracy(X, y_onehot)
print(f"\nTOTAL PENGUIN ACCURACY: {total_acc:.1f}%")

Steg 4

Du kan också visualisera din pingvin-hjärnas respektive perceptroners skiljelinjer om du tar denna kod och lägger till i programmet (inte i din PenguinNetwork klass)

def plot_brainiac_decision_boundaries(brain, X, y_onehot):
    plt.figure(figsize=(10, 6))

    # 1. Plotta alla pingviner
    # Vi måste göra om One-Hot till vanliga klass-namn för att färglägga
    y_labels = [brain.species_names[np.argmax(row)] for row in y_onehot]
    sns.scatterplot(x=X[:, 0], y=X[:, 1], hue=y_labels, palette="deep")

    # 2. Rita linjer för varje perceptron
    colors = ["blue", "orange", "green"] # Matchar ofta Seaborns palette

    x_range = np.array([0, 1]) # Eftersom vi normaliserat är datat mellan 0 och 1

    for i, p in enumerate(brain.perceptrons):
        weights = p.weights
        bias = p.bias

        # Linjens ekvation: w1*x + w2*y + bias = 0
        # Lös ut y: y = -(w1*x + bias) / w2

        # Skydd mot division med noll (om vikten är 0 är linjen vertikal)
        if abs(weights[1]) > 0.001:
            y_range = -(weights[0] * x_range + bias) / weights[1]

            plt.plot(x_range, y_range, label=f"{brain.species_names[i]} Gräns",
                     color=colors[i], linestyle="--", linewidth=2)
        else:
            print(f"Kunde inte rita linje för {brain.species_names[i]} (vertikal linje)")

    plt.xlabel("Flipper Length (Norm)")
    plt.ylabel("Bill Length (Norm)")
    plt.ylim(0, 1) # Håll grafen inom rimliga gränser
    plt.xlim(0, 1)
    plt.legend()
    plt.title("Perceptronernas Beslutsgränser")
    plt.show()

# Kör visualiseringen
plot_brainiac_decision_boundaries(brain, X, y_onehot)

Steg 5: Hitta konflikter

Testa gissa på fler pingviner i ditt träningsdata. Du kommer snart hitta fall där svaret blir [1, 1, 0] eller [0, 0, 0].

[1, 1, 0]: Både Adelie-experten och Chinstrap-experten skriker "JA!". Vem ska vi lita på?
[0, 0, 0]: Ingen känner igen pingvinen.

Vi behöver en bättre strategi för att avgöra vem vi kan lita på mest!

Övning 3: Uppgraderingen (Sigmoid)

Lösning: För att lösa konflikten måste vi byta ut den hårda steg-funktionen mot den mjuka Sigmoid-funktionen. Istället för att svara 1 (Ja), svarar perceptronen kanske 0.98 (98% säker på Ja).

Uppdatera Perceptronen: Gå in i din Perceptron-klass och ändra activate så att den returnerar sigmoid-värdet (float) istället för 1/0.

Troligen behöver du något i stil med detta:
```
def activate(self, value):
    return 1 / (1 + math.exp(-value))  # kläm ihop mellan 0 och 1
```
Testa ditt nätverk: Nu får du tre siffror, t.ex: [0.92, 0.55, 0.02]. Både Adelie (0.92) och Chinstrap (0.55) hade sagt "Ja" med den gamla metoden (eftersom båda är över 0.5, notera att sigmoid(0) = 0.5). Men nu ser vi tydligt att Adelie är vinnaren.

Vissa vill i det här läget ha en ny metod i PenguinNetwork som heter predict_winner som hittar den högsta siffran i listan och returnerar rätt namn ("Adelie").
```
def predict_winner(self, input_data):
    """Returnerar namnet på den art som fick högst poäng."""
    probs = self.predict(input_data)
    winner_index = np.argmax(probs) # Indexet för högsta värdet
    return self.species_names[winner_index]
```

Övning 4: SimpleNeuralNetwork (Generalisering)

Syfte: Att skriva en ny klass för varje problem (PenguinNetwork, TitanicNetwork...) är jobbigt. Vi vill ha en generell klass som kan skapa hur många perceptroner som helst beroende på problemet.

Vi kallar den SimpleNeuralNetwork. Det är i princip exakt samma kod som PenguinNetwork, men vi byter ut det hårda värdet 3 mot variabeln num_outputs.

Detta är början på ett riktigt Neuralt Nätverk (ett nätverk med ett enda lager).

Din uppgift: Bygg klassen SimpleNeuralNetwork.

class SimpleNeuralNetwork:
    def __init__(self, num_inputs, num_outputs):
        # TODO: Skapa en lista 'self.perceptrons' med 'num_outputs' st perceptroner
        pass

    def predict(self, inputs):
        # TODO: Returnera en lista med alla perceptronernas sigmoid-svar
        pass

    def train(self, inputs, targets):
        # TODO: Träna varje perceptron mot sin motsvarande kolumn i targets
        pass

Övning 5: Upp till bevis

Nu har du ett generellt nätverk. Låt oss se vad det klarar av!

Test A: Cancer-diagnostik (30 dimensioner) Datasetet "Breast Cancer Wisconsin" har 30 inputs. Är det för svårt för din enkla modell?

Ladda data: from sklearn.datasets import load_breast_cancer.
- df = sklearn.datasets.load_breast_cancer(as_frame=True)
Normalisera!
Resultat: Du bör få över 90% rätt. Medicinsk data är ofta linjärt separerbar!

Test B: Handskrivna Siffror (Digits) Ladda med df = sklearn.datasets.load_digits(as_frame=True).

Data: 64 inputs (pixlar).
Facit: 10 outputs (siffrorna 0-9). Du måste one-hot encoda facit.
Resultat: Du bör få ca 95% rätt! Det visar att handstil faktiskt är ganska linjärt (en nolla ser annorlunda ut än en etta på ett förutsägbart sätt).

Test C: Det omöjliga problemet (XOR) Skapa data för XOR: [[0,0], [0,1], [1,0], [1,1]] med facit [[1,0], [0,1], [0,1], [1,0]].

Resultat: Här tar det stopp. Nätverket kommer gissa fel eller vara väldigt osäkert (runt 0.5 på allt).

Slutsats: Vi har bevisat att din kod kan rädda liv (Cancer) och läsa handstil (Digits). Men den kan inte lösa enkel logik (XOR). Varför? För att din modell består av raka linjer. För att lösa XOR (och cirklar) måste vi kunna böja rymden. Vi behöver Dolda Lager.

Övning 6: XOR med gömda lager

I denna uppgift får du testa skapa ett första gömt lager. Tanken är såhär. Vissa samband kan vi bara uttrycka om flera neuroner jobbar tillsammans. Om output från ett första lager neuroner, kan skickas som input till nästa lager, kan fler och mer avancerade samband representeras. I följande exempel får du ett nätverk som har 3 neuroner i sig, kapabla att representera de logiska operationerna NAND, OR, och AND. Genom att använda dem tillsammans kan du implementera en XOR.

import numpy as np

class Neuron:
    def __init__(self, weights, bias):
        self.weights = weights
        self.bias = bias

    def predict(self, inputs):
        total = np.dot(inputs, self.weights) + self.bias
        return total > 0


class XORNetwork:
    def __init__(self):
        self.nand_neuron = Neuron(weights=[-0.5, -0.5], bias=0.75)
        self.or_neuron = Neuron(weights=[0.5, 0.5], bias=-0.25)
        self.and_neuron = Neuron(weights=[0.5, 0.5], bias=-0.75)

    def predict(self, inputs):
        # TODO: USE THE NEURONS IN A CLEVER WAY TO MAKE THE NETWORK RETURN THE PROPER
        # XOR SOLUTION
        pass


# --- Testa det nätverket med XOR-data ---
print("--- Test ---")
xor_inputs = [[0, 0], [0, 1], [1, 0], [1, 1]]
xor_targets = [0, 1, 1, 0]  # Facit för XOR

network = XORNetwork()

for input_data, target in zip(xor_inputs, xor_targets):
    prediction = network.predict(input_data)
    print(f"Input: {input_data}, Facit: {target}, Prediktion: {prediction:.0f}")

Övning 7: XOR med gömda lager SOM LÄR SIG

I denna övning får du en uppsättning TODO:s att lösa så får du skriva backpropagation koden för ett simpelt XOR nätverk. På detta sett får du en första erfarenhet med att använda sigmoid derivator för att hitta ett "delta", som vi också kan kalla "felansvar". Och beräkna detta delta både för output samt gömda lager.

import random
import math
import numpy as np

random.seed(42)

def sigmoid(x):
    if x < -700:
        return 0.0
    if x > 700:
        return 1.0
    return 1 / (1 + math.exp(-x))

def sigmoid_derivative(sig_output):
    return sig_output * (1 - sig_output)


class Neuron:
    def __init__(self, num_inputs):
        self.weights = [random.uniform(-1, 1) for _ in range(num_inputs)]
        self.bias = random.uniform(-1, 1)

    def predict(self, inputs):
        total = np.dot(inputs, self.weights) + self.bias
        return sigmoid(total)


class XORNetwork:
    def __init__(self):
        # Vi skapar de tre neuronerna explicit
        self.hidden1 = Neuron(num_inputs=2)
        self.hidden2 = Neuron(num_inputs=2)
        self.output_neuron = Neuron(num_inputs=2)

    def predict(self, inputs):
        # Manuell framåtmatning
        h1_out = self.hidden1.predict(inputs)
        h2_out = self.hidden2.predict(inputs)
        final_out = self.output_neuron.predict([h1_out, h2_out])
        return final_out

    def train(self, inputs, targets, epochs, learning_rate):
        for epoch in range(epochs):
            for x, target in zip(inputs, targets):
                h1_out = self.hidden1.predict(x)
                h2_out = self.hidden2.predict(x)
                final_out = self.output_neuron.predict([h1_out, h2_out])

                # TODO 1: Beräkna felet i sista lagret som facit - output

                # TODO 2: Beräkna "delta" - felansvaret som (error * derivatan av aktiveringsfunktionen)

                # TODO 3: Beräkna felet för varje hidden neuron genom att
                # titta på varje neuron som den skickar sin output till
                # hämta vikten från den mottagande neuronen som den använder för motsvarande input
                # hämta delta från den mottagande neuronen
                # multiplicera denna vikt med detta delta
                # om det är flera neuroner som tar emot outputten så summeras dessa värden
                # i deta exempel är det alltså self.output_neuron.weights[0] för self.hidden1

                # TODO 4: Beräkna varje hidden neurons delta genom att multiplicera dess error 
                # med sigmoid derivatan för dess output

                # TODO 5: Uppdatera varje vikt i varje neuron genom att ta:
                # vikt_för_input_x += learning*rate * delta_neuron * input_x
                # där input_x är det input som användes för den vikten under senaste körningen
                # alltså t.ex. variabel x[0] för hidden1.weights[0] och h1_out för output_neuron.weights[0]

                # TODO 6: Beräkna bias för varje neuron som:
                # neuron_bias += learning_rate * neuron_delta



                


# --- KÖRNING ---
xor_inputs = [[0, 0], [0, 1], [1, 0], [1, 1]]
xor_targets = [0, 1, 1, 0]

network = XORNetwork()

network.train(xor_inputs, xor_targets, epochs=10000, learning_rate=0.5)

print("\n--- Resultat (Specialiserat XOR-nätverk) ---")
for x, t in zip(xor_inputs, xor_targets):
    pred = network.predict(x)
    print(f"Input: {x}, Facit: {t}, Prediktion: {pred:.4f}")

Övning 8: Ett generellt neuralt nätverk

Vi börjar närma oss nu! I nästa exempel ska du få skriva ett fullt kapabelt neuralt nätverk som kan ha ett variabelt antal gömda inputs, outputs och gömda lager.

Lös följande TODOS och ta din tid. Du skapar något nu som du kommer kunna använda länge.

import numpy as np
import random
import math

random.seed(42)

def sigmoid(x):
    if x < -700:
        return 0.0
    if x > 700:
        return 1.0
    return 1 / (1 + math.exp(-x))

def sigmoid_derivative(sig_output):
    return sig_output * (1 - sig_output)

class Neuron:
    def __init__(self, num_inputs):
        self.weights = [random.uniform(-1, 1) for _ in range(num_inputs)]
        self.bias = random.uniform(-1, 1)


    def predict(self, inputs):
        total = np.dot(inputs, self.weights)
        total += self.bias
        return sigmoid(total)


class NeuralNetwork:
    def __init__(self, layer_sizes):
        self.layers = []
        # skapa alla lager med rätt storlekar
        for i in range(1, len(layer_sizes)):
            num_inputs = layer_sizes[i - 1]
            num_neurons = layer_sizes[i]
            self.layers.append([Neuron(num_inputs) for _ in range(num_neurons)])

    def predict(self, inputs):
        # kör igenom alla lager, output från ett lager blir input till nästa
        current_inputs = inputs
        for layer in self.layers:
            next_inputs = [neuron.predict(current_inputs) for neuron in layer]
            current_inputs = next_inputs
        return current_inputs

    def train(self, inputs, targets, epochs, learning_rate):
        for epoch in range(epochs):
            for x, target in zip(inputs, targets):
                # --- 1. Forward Pass ---
                # kör samma kod som i vår predict, men spara på oss outputs från varje lager.

                inputs_to_layer = [x]
                current_inputs = x
                for layer in self.layers:
                    layer_outputs = [n.predict(current_inputs) for n in layer]
                    inputs_to_layer.append(layer_outputs)
                    current_inputs = layer_outputs

                # --- 2. Backward Pass ---

                # Vi börjar med att beräkna samtliga deltas för sista lagret
                output_deltas = []
                
                # Hämta deltas för varje neuron i output lager
                for i, neuron in enumerate(self.layers[-1]):
                    # Facit för just denna output-neuron
                    t = target[i]
                    # Gissningen från just denna output-neuron
                    y = inputs_to_layer[-1][i] # -1 som index på en lista betyder "sista"

                    # TODO 1: Beräkna error för neuronen

                    # TODO 2: Beräkna delta för neuronen och spara i output_deltas

                

                # Starta deltas-listan med output-lagrets deltas
                deltas = [output_deltas]

                # B. Dolda lager (Baklänges)
                for i in range(len(self.layers) - 2, -1, -1):
                    current_layer = self.layers[i] # Håll koll på det nuvarande lagret
                    next_layer = self.layers[i + 1] # Referens till noderna i lagret efter
                    next_deltas = deltas[0] # Referens till deltas i lagret efter 
                    current_deltas = [] # lista som vi kommer spara varje delta i nuvarandde lager i
                    current_outputs = inputs_to_layer[i + 1]

                    # för varje neuron i nuvarande lager, beräkna först error, sen delta
                    for j, neuron in enumerate(current_layer):

                        # TODO 3: Loopa över nästa lager noder. För varje nod, multiplicera dess weights[j] med dens delta
                        # summera alla dessa produkter
                
                        # TODO 4: beräkna deltat som summan * sigmoid_derivatan för neuronens output
                        # lägg tll deltat till current_deltas
                        pass # TODO: ta bort "pass" när du är klar med koden
                    
                    # TODO 5: lägg till current_deltas längst fram i listan deltas

                # --- 3. Update Weights ---
                for i, layer in enumerate(self.layers):
                    for j, neuron in enumerate(layer):
                        # TODO 6: Hämta ut delta för neuron j i lager i
                        
                        # TODO 7: Hämta alla inputs till lager i 

                        # TODO 8: För alla neuronens vikter:
                            # neuron.vikt += learning_rate * neuron_delta * input för motsvarande vikt
                        
                        # TODO 9: uppdatera bias
                        # neuron.bias += learning_rate * neuron_delta
                        
                        pass # TODO: ta bort "pass" när du är klar


# --- TEST ---

xor_inputs = [[0, 0], [0, 1], [1, 0], [1, 1]]

xor_targets = [[0], [1], [1], [0]]

network = NeuralNetwork([2, 2, 1])

# SGD-träning
network.train(xor_inputs, xor_targets, epochs=10000, learning_rate=0.5)

print("\n--- Resultat ---")
for x, t in zip(xor_inputs, xor_targets):
    # predict returnerar nu en lista, t.ex. [0.043]
    pred_list = network.predict(x)
    pred_value = pred_list[0]
    print(f"Input: {x}, Facit: {t}, Prediktion: {pred_value:.4f}")

Övning 9: Modifiera ett Neuralt Nätverk

Syfte: Att förstå hur arkitekturen i ett neuralt nätverk påverkar dess förmåga att lära sig, genom att modifiera olika parametrar.

Använd NeuralNetwork-koden: Använd koden som du precis skrivit.
Experiment 1: Färre Neuroner. Ändra arkitekturen från [2, 2, 1] (två input, två dolda, en output) till [2, 1, 1]. Du har nu skapat en "flaskhals" med bara en enda neuron i det dolda lagret. Kör träningskoden igen. Kan nätverket fortfarande lösa XOR? Varför/varför inte?
Experiment 2: Djupare Nätverk. Ändra arkitekturen till [2, 4, 4, 1]. Du har nu skapat ett djupare nätverk med två dolda lager. Träna modellen igen. Lär den sig snabbare eller långsammare? Blir resultatet mer stabilt?

Reflektera

Du har nu agerat som en AI-arkitekt. Hur påverkade antalet neuroner och lager modellens prestanda? Detta är kärnan i hyperparameter-tuning: att hitta den bästa arkitekturen och de bästa inställningarna för ett givet problem.

Övning 10: "Hello World" för Neurala Nätverk (Siffror)

Syfte: Att binda ihop allt genom att använda vår NeuralNetwork-klass för att lösa ett klassiskt problem: Läsa handskrivna siffror. Här måste du använda One-Hot encoding fullt ut.

Ladda dataset: Använd sklearn.datasets.load_digits(as_frame=True). Detta innehåller 8x8 pixlar stora bilder av siffror (0-9).
Förbered Data:
- Normalisera: Dela alla pixelvärden med 16 (eftersom maxvärdet i detta dataset är 16) så de hamnar mellan 0-1.
- One-Hot Encode: Skapa facit. Om siffran är 2, ska facit vara [0, 0, 1, 0, 0, 0, 0, 0, 0, 0].
Träna:
- Skapa ett nätverk: nn = NeuralNetwork([64, 30, 10]) (64 inputs, 30 dolda, 10 outputs).
- Kör .fit().
Testa:
- Ta en siffra från testdatan.
- Kör nn.predict().
- Du får tillbaka en lista med 10 sannolikheter. Använd argmax (hitta största värdet) för att se vad nätverket gissade.

from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split

# 1. Ladda data
digits = load_digits()
X = digits.data  # 1797 bilder, 64 pixlar per bild
y_raw = digits.target # Siffrorna 0-9

# 2. Normalisera (0-16 -> 0.0-1.0)
X = X / 16.0

# 3. One-Hot Encoding (Manuell version för förståelse)
y_onehot = []
for label in y_raw:
    # Skapa en lista med 10 nollor
    vector = [0.0] * 10
    # Sätt en 1:a på rätt plats
    vector[label] = 1.0
    y_onehot.append(vector)

# Dela upp i train/test
X_train, X_test, y_train, y_test = train_test_split(X, y_onehot, test_size=0.2, random_state=42)

# 4. Träna nätverket
# Input: 64 (pixlar), Hidden: 16 (godtyckligt), Output: 10 (siffror)
nn = NeuralNetwork([64, 16, 10])
nn.fit(X_train, y_train, epochs=2000, learning_rate=0.5)

# 5. Utvärdera
correct = 0
for i in range(len(X_test)):
    prediction = nn.predict(X_test[i])
    # Hitta indexet med högst värde (ArgMax)
    guessed_digit = prediction.index(max(prediction))
    actual_digit = y_test[i].index(max(y_test[i]))

    if guessed_digit == actual_digit:
        correct += 1

print(f"Noggrannhet: {(correct / len(X_test)) * 100:.1f}%")

Övning 11: Nya problem, samma kod

Grattis! Du har nu kodat ett fullt fungerande Neuralt Nätverk från grunden. Det coola är att matematiken inte bryr sig om vad siffrorna representerar. Pixlar? Pengar? Temperatur? Allt är bara listor med tal.

Hittills har vi gjort Klassificering (Svart/Vitt, Katt/Hund, Siffra 0-9). Men kan vi använda samma kod för att förutsäga framtiden?

Scenario A: Regression (Förutsäga Huspriser)

Att gissa ett flyttal (t.ex. temperatur eller pris) kallas Regression. Vi har dock ett litet problem. Din Neuron-klass slutar med en sigmoid-funktion. Den klämmer alltid in svaret mellan 0.0 och 1.0.

Om vi vill gissa priset på ett hus i Kalifornien (där priserna är i hundratusentals dollar), kommer neuronen slå i taket vid 1.0.

Tricket: Vi måste normalisera facit.

Om dyraste huset kostar 500 000 dollar, låtsas vi att det kostar 1.0.
Vi tränar nätverket.
När nätverket gissar 0.5, betyder det "50% av maxpriset". Vi multiplicerar då svaret med 500 000 för att få det riktiga priset.

Låt oss testa detta på det kända datasetet California Housing.

from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
import numpy as np

# 1. Ladda data (20,000 hus, 8 features per hus)
housing = fetch_california_housing()
X = housing.data
y = housing.target.reshape(-1, 1) # Facit är huspriser (i $100,000-tal)

print(f"Exempel data: {X[0]}")
print(f"Exempel pris: {y[0]}")

# 2. NORMALISERA ALLT (Inputs OCH Targets)
# Vi måste skala ner priserna (y) till 0-1 för att Sigmoid ska funka!
x_min, x_max = X.min(axis=0), X.max(axis=0)
y_min, y_max = y.min(axis=0), y.max(axis=0)

X_scaled = (X - x_min) / (x_max - x_min)
y_scaled = (y - y_min) / (y_max - y_min)

# Dela upp i train/test
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y_scaled, test_size=0.2)

# 3. Skapa nätverket
# 8 inputs (rum, ålder, läge, etc...), 10 dolda neuroner, 1 output (pris)
regressor = NeuralNetwork([8, 10, 1])

print("Tränar bostadsmäklaren...")
regressor.train(X_train, y_train, epochs=2000, learning_rate=0.1)

# 4. Testa och översätt tillbaka!
print("\n--- Testar på okända hus ---")
predictions_scaled = []
for i in range(5): # Testa på 5 hus
    # Gissning (0.0 - 1.0)
    pred_scaled = regressor.predict(X_test[i])[0] 
    
    # Översätt tillbaka till riktiga pengar (Inverse Transform)
    # Formel: scaled * (max - min) + min
    price_guess = pred_scaled * (y_max - y_min) + y_min
    price_real = y_test[i] * (y_max - y_min) + y_min
    
    print(f"Gissning: ${price_guess[0]*100000:.0f}, Riktigt pris: ${price_real[0]*100000:.0f}")

Om gissningarna är någorlunda nära har ditt klassificerings-nätverk precis blivit en fastighetsmäklare!

Scenario B: Vin (Multi-class)

Låt oss återvända till klassificering men göra det lite svårare. Datasetet Wine innehåller kemisk analys av tre olika vinsorter.

Här måste vi använda One-Hot Encoding igen, eftersom vi har 3 klasser.

from sklearn.datasets import load_wine

# 1. Ladda data
wine = load_wine()
X = wine.data
y = wine.target # 0, 1, eller 2

# 2. Normalisera Inputs
X = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))

# 3. One-Hot Encode Targets
# Vi behöver göra om 0 -> [1,0,0], 1 -> [0,1,0], etc.
y_onehot = []
for label in y:
    vec = [0, 0, 0]
    vec[label] = 1
    y_onehot.append(vec)

# Dela upp
X_train, X_test, y_train, y_test = train_test_split(X, y_onehot, test_size=0.3)

# 4. Träna Sommelieren
# Wine har 13 features (alkoholhalt, syra, färg, etc)
# Vi vill ha 3 outputs (en sannolikhet för varje vinsort)
sommelier = NeuralNetwork([13, 8, 3]) 

print("Tränar Sommelieren...")
sommelier.train(X_train, y_train, epochs=3000, learning_rate=0.2)

# 5. Utvärdera
correct = 0
for i in range(len(X_test)):
    probs = sommelier.predict(X_test[i])
    guess = probs.index(max(probs)) # Hitta indexet med högst sannolikhet
    actual = y_test[i].index(1)     # Hitta var 1:an sitter i facit
    
    if guess == actual:
        correct += 1

print(f"Sommelieren hade rätt på {correct} av {len(X_test)} viner.")
print(f"Accuracy: {(correct/len(X_test))*100:.1f}%")

Utforskaren: Dataset-menyn

Nu är det din tur. Din kod fungerar på nästan allt. Här är en "meny" av inbyggda dataset i sklearn som du kan testa att ladda in och lösa med din NeuralNetwork-klass. Kom ihåg de två gyllene reglerna:

Normalisera alltid X (Inputs).
Om Klassificering: One-Hot Encoda Y.
Om Regression: Normalisera Y (och skala tillbaka svaret sen).

Dataset	Typ	Kod för att ladda	Utmaning
Diabetes	Regression	`sklearn.datasets.load_diabetes()`	Gissa sjukdomsutveckling baserat på blodvärden.
Olivetti Faces	Bild-Klassificering	`sklearn.datasets.fetch_olivetti_faces()`	Svår! 4096 inputs (pixlar), 40 olika personer. Kräver ett stort nätverk!

Gör så här: Välj ett dataset från listan. Kopiera koden från Scenario A (för Regression) eller Scenario B (för Klassificering) och byt bara ut raden där du laddar datan. Lycka till!

Övning 12: Kan ditt nätverk läsa?

För att mata in text i vårt nätverk använder vi en klassisk teknik som heter Bag of Words. Tänk dig att vi tar en mening, klipper ut alla ord, och lägger dem i en påse. Vi bryr oss inte om ordningen, bara vilka ord som finns med.

Strategin:

Ordbok: Vi skapar en lista på alla unika ord nätverket känner till.
Översättning: Varje mening blir en lista med ettor och nollor.
- Om ordboken är ["bra", "dåligt", "mat"].
- Meningen "bra mat" blir [1, 0, 1].
- Meningen "dåligt" blir [0, 1, 0].

Låt oss koda detta!

import numpy as np

# --- 1. Vårt lilla dataset ---
# Meningar (Inputs)
sentences = [
    "jag älskar detta",
    "detta är fantastiskt",
    "vilken underbar dag",
    "maten var god",
    "jag hatar detta",
    "detta är hemskt",
    "vilken hemsk dag",
    "maten var äcklig"
]

# Facit (Targets): 1 = Positivt, 0 = Negativt
labels = [
    [1], [1], [1], [1],  # De 4 första är positiva
    [0], [0], [0], [0]   # De 4 sista är negativa
]

# --- 2. Bygg Ordboken (Vocabulary) ---
# Splitta alla meningar till ord och hitta unika ord
vocabulary = set()
for s in sentences:
    for word in s.split():
        vocabulary.add(word)

vocabulary = list(vocabulary) # Gör om till lista så ordningen är fast
print(f"Nätverket kan {len(vocabulary)} ord: {vocabulary}")

# --- 3. Hjälpfunktion: Text till Siffror ---
def text_to_vector(text):
    # Skapa en lista med nollor, lika lång som ordboken
    vector = [0] * len(vocabulary)
    words = text.split()
    for word in words:
        if word in vocabulary:
            # Hitta vilken plats ordet har i ordboken
            index = vocabulary.index(word)
            # Sätt en 1:a på den platsen
            vector[index] = 1
    return vector

# Testa funktionen
print(f"\nTest: 'jag hatar' -> {text_to_vector('jag hatar')}")

# --- 4. Förbered träningsdatan ---
X_train = [text_to_vector(s) for s in sentences]
y_train = labels

# --- 5. Träna Nätverket ---
# Input size = Antal ord i ordboken. Output = 1 (Positiv/Negativ).
nn = NeuralNetwork([len(vocabulary), 4, 1])

print("\nLär nätverket svenska...")
nn.train(X_train, y_train, epochs=2000, learning_rate=0.1)

# --- 6. Testa på NYA meningar ---
print("\n--- Testar nätverkets språkkänsla ---")

test_sentences = [
    "jag älskar maten",  # En mix av ord den sett i positiva sammanhang
    "detta är äckligt",  # En mix av ord den sett i negativa sammanhang
    "jag hatar maten",   # Ny kombination
]

for s in test_sentences:
    vec = text_to_vector(s)
    prediction = nn.predict(vec)[0] # Få ut talet
    
    # Tolka resultatet
    sentiment = "POSITIV :)" if prediction > 0.5 else "NEGATIV :("
    print(f"Mening: '{s}' -> Gissning: {prediction:.2f} -> {sentiment}")

Analys: Vad hände precis?

Om du kör koden kommer du se att nätverket troligen gissar rätt på "jag älskar maten", trots att den meningen aldrig fanns i träningsdatan!

Hur?

Nätverket lärde sig att ordet "älskar" har en stark koppling till positiv output (1).
Det lärde sig att "maten" är neutralt (finns i både bra och dåliga meningar).
När du kombinerar dem väger "älskar" tyngre, och summan blir positiv.

Du har precis byggt en AI som förstår (vissa) ords innebörd baserat på erfarenhet!

Begränsningen (Varför detta inte är ChatGPT)

Ditt nätverk använder "Bag of Words". Det betyder att den tappar bort ordföljden. För ditt nätverk betyder följande två meningar exakt samma sak, eftersom de innehåller samma ord:

"Mat var inte bra, den var dålig"
"Mat var inte dålig, den var bra"

För att förstå skillnaden här (där ordet "inte" negerar ordet som kommer efter), behöver man nätverk som har minne och läser ord i sekvens (som RNN eller Transformers/GPT). Men grundprincipen är densamma: Text måste bli siffror för att maskinen ska fatta.

Övning 13: Spionkameran (Autoencoder & Denoising)

Hittills har vi matat in en bild och fått ut en etikett ("Det är en femma"). Men vad händer om input är en bild och output också är en bild?

Detta kallas för en Autoencoder. Det används för att restaurera gamla foton, ta bort brus, eller komprimera data.

Uppdraget: Du är en underrättelseofficer. Dina spionsatelliter skickar ner bilder på siffror, men atmosfären lägger till massa "brus" (myrornas krig) på bilderna. Din chef vill ha rena bilder. Vi ska träna nätverket att:

Ta emot en trasig bild.
Pressa informationen genom ett litet "hål" (få neuroner).
Rekonstruera en hel bild på andra sidan.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split

# 1. Ladda data
digits = load_digits()
X = digits.data / 16.0 # Normalisera 0-1

# 2. Skapa "trasig" data (Lägg till brus)
# Vi lägger till slumpmässiga tal på alla pixlar
noise_factor = 0.5
X_noisy = X + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=X.shape) 
# Klipp värdena så de fortfarande är mellan 0 och 1
X_noisy = np.clip(X_noisy, 0., 1.)

# Dela upp: X_train_noisy är INPUT, X_train_clean är FACIT
X_train_noisy, X_test_noisy, X_train_clean, X_test_clean = train_test_split(
    X_noisy, X, test_size=0.2, random_state=42
)

# 3. Bygg Autoencodern
# Input: 64 pixlar
# Hidden: 32 neuroner (Vi tvingar nätverket att komprimera bilden!)
# Output: 64 pixlar (Vi vill ha ut en bild igen)
autoencoder = NeuralNetwork([64, 32, 64])

print("Tränar på att ta bort brus...")
# Notera: Vi tränar med NOISY som input och CLEAN som target!
autoencoder.train(X_train_noisy, X_train_clean, epochs=1000, learning_rate=0.1)

# 4. Visualisera Resultatet
print("Visar resultat...")

# Välj 5 slumpmässiga bilder från test-setet
idxs = np.random.randint(0, len(X_test_noisy), 5)

plt.figure(figsize=(10, 4))
for i, idx in enumerate(idxs):
    # A. Den trasiga bilden (Input)
    ax = plt.subplot(3, 5, i + 1)
    plt.imshow(X_test_noisy[idx].reshape(8, 8), cmap="gray")
    ax.axis("off")
    if i == 2: ax.set_title("Input (Brusig)")

    # B. Nätverkets lagning (Output)
    # OBS: Predict ger en lista, vi måste göra om den till numpy array för att kunna reshapea
    reconstructed = np.array(autoencoder.predict(X_test_noisy[idx]))
    
    ax = plt.subplot(3, 5, i + 1 + 5)
    plt.imshow(reconstructed.reshape(8, 8), cmap="gray")
    ax.axis("off")
    if i == 2: ax.set_title("Output (Lagad)")

    # C. Facit (Originalet)
    ax = plt.subplot(3, 5, i + 1 + 10)
    plt.imshow(X_test_clean[idx].reshape(8, 8), cmap="gray")
    ax.axis("off")
    if i == 2: ax.set_title("Original (Facit)")

plt.show()

Övning 14: Sinus

Det finns en matematisk sats som heter "Universal Approximation Theorem". Den säger att ett neuralt nätverk med minst ett dolt lager kan lära sig vilken matematisk funktion som helst, oavsett hur konstig den ser ut.

Låt oss bevisa det genom att lära nätverket en Sinuskurva. Det här är grunden för hur AI styr robotar (mjuka rörelser) eller förutspår aktiekurser (svängningar).

Problemet är detsamma som med huspriserna: Sinus går mellan -1 och 1. Vår Sigmoid går mellan 0 och 1. Vi måste "flytta upp" sinuskurvan så den passar nätverket.

import numpy as np
import matplotlib.pyplot as plt

# 1. Skapa Data: En Sinusvåg
# X är värden mellan 0 och 2*PI (en hel våg)
X = np.linspace(0, 2 * np.pi, 100).reshape(-1, 1) # 100 punkter
y = np.sin(X)

# 2. Normalisera för Sigmoid
# Sinus går från -1 till 1. Vi flyttar det till 0 till 1.
# Formel: (y + 1) / 2
y_shifted = (y + 1) / 2
X_normalized = X / (2 * np.pi) # Normalisera X också till 0-1 för snabbare träning

# 3. Bygg Nätverket
# 1 Input (x-värdet)
# 10 Dolda neuroner (för att kunna böja linjen mjukt)
# 1 Output (y-värdet)
math_brain = NeuralNetwork([1, 10, 1])

print("Lär nätverket att rita vågor...")
# Vi behöver många epoker för att få en mjuk kurva
math_brain.train(X_normalized, y_shifted, epochs=10000, learning_rate=0.1)

# 4. Förutsäg och Rita
predictions = []
for val in X_normalized:
    pred = math_brain.predict(val)
    predictions.append(pred[0])

# Gör om till numpy array
predictions = np.array(predictions)

# Plotta
plt.figure(figsize=(10, 6))
plt.scatter(X, y_shifted, label="Facit (Sinus)", color="gray", s=10)
plt.plot(X, predictions, label="Nätverkets gissning", color="red", linewidth=3)
plt.title("Neuralt Nätverk lär sig Sinus-funktionen")
plt.legend()
plt.show()

Övning 15: Tolka ett Beslutsträd

Syfte: Att översätta det visuella beslutsträdet från läroboken till en uppsättning läsbara IF/ELSE-regler, för att bevisa dess status som en "white box"-modell.

Kör koden: Kör Python-koden från "Fallstudie 2: Beslutsträd i Praktiken" i textboken för att generera bilden av det tränade Iris-trädet.
Analysera bilden: Titta på den översta noden (roten).
- Vilken fråga ställer den? (t.ex. petal length (cm) <= 2.45).
- Om True, vart leder den? Om False, vart leder den?
Skriv ner reglerna: Följ varje möjlig väg från roten ner till ett löv och skriv ner det som en IF/ELSE-sats i pseudokod eller vanlig text.
- Exempel på en regel:
```
IF petal length <= 2.45 THEN
    CLASSIFY AS: setosa
ELSE
    IF petal width <= 1.75 THEN
        ... (fortsätt följa trädet)
```
Jämför: Har du nu en komplett uppsättning regler som exakt beskriver hur modellen fattar sina beslut?

Reflektera

Jämför detta med det neurala nätverket. Skulle du kunna göra samma sak där – titta på de inlärda vikterna och bias-värdena och skriva ner en uppsättning enkla, mänskligt läsbara regler? Varför är denna egenskap (tolkningsbarhet) så viktig i vissa tillämpningar, som medicinsk diagnostik eller kreditbedömning?

Övning 16: Konsten att Välja rätt 'K'

Syfte: Att utforska en av de största utmaningarna med K-Means clustering: att i förväg veta hur många kluster (K) man ska leta efter.

Använd K-Means-koden: Ta koden från "Fallstudie: K-Means Clustering i Praktiken" i textboken. Den använder make_blobs för att skapa data med 4 tydliga kluster.
Experimentera med K:
- Kör koden precis som den är, med n_clusters=4. Resultatet bör se perfekt ut.
- Ändra nu n_clusters till 2. Kör igen. Hur försöker algoritmen tvinga in datan i bara två grupper?
- Ändra n_clusters till 8. Kör igen. Vad händer nu? Ser du hur några av de naturliga klustren har blivit godtyckligt uppdelade?
Visualisera: Spara bilderna från varje körning och jämför dem sida vid sida.

Reflektera

Denna övning visar att även om K-Means är kraftfullt, kräver det ofta mänsklig expertis för att välja rätt hyperparametrar. I verkliga dataset (som kunddata) vet man sällan det "rätta" antalet kluster i förväg. Hur skulle du kunna gå tillväga för att hitta ett rimligt K för ett helt okänt dataset? (Detta är ett aktivt forskningsområde, med metoder som "Elbow Method" och "Silhouette Score").

Övning 17: Skogarnas Kamp

Syfte: Att jämföra prestandan mellan ett enkelt Beslutsträd och en Random Forest, och se hur ensemble-metoder kan minska variansen (göra modellen stabilare).

Skapa en fil: forest_battle.py.

Förbered data: Använd make_moons från sklearn.datasets för att skapa ett dataset som är lite svårare än Iris (det är inte linjärt separerbart och har lite brus).

from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score

# Skapa data som ser ut som två månar (svårt för raka linjer)
X, y = make_moons(n_samples=500, noise=0.30, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

Träna modellerna:
- Träna en DecisionTreeClassifier.
- Träna en RandomForestClassifier (t.ex. med 100 träd).
Jämför: Beräkna och skriv ut accuracy_score för båda på testdatan.
Analysera: Vilken modell vann? Random Forest bör vara mer robust mot bruset i datan.

Övning 18: Titanic med RandomForest

Syfte: Att tillämpa "Hantverket" (datarensning, hantering av kategorier) på ett klassiskt dataset: Titanic.

Skapa en fil: titanic_survival.py.
Ladda ner daxta: Använd Seaborn för att hämta titanic datat som i uppgift 2.

Använd Pandas:

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
import seaborn as sns

# 1. Ladda data
df = sns.load_dataset("titanic")

# 2. Titta på datan
print(df.head())
print(df.isnull().sum()) # Kolla efter saknade värden

Städa data (Hantverket):
- Välj relevanta kolumner (t.ex. Pclass, Sex, Age, SibSp, Parch, Fare).
- Hantera NaNs: Fyll i saknade åldrar med medelåldern (df['Age'].fillna(df['Age'].mean(), inplace=True)).
- Hantera Text: Omvandla 'Sex' till siffror (male=0, female=1) eller använd pd.get_dummies.
Träna och Testa:
- Dela upp i X (features) och y (survived).
- Kör train_test_split.
- Träna en RandomForestClassifier.
- Utvärdera. Vad påverkade överlevnadschansen mest? (Tips: kolla clf.feature_importances_).

Övning 19: Avslöja Dolda Strukturer med PCA

Syfte: Att använda PCA för att visualisera ett högdimensionellt dataset (handskrivna siffror) och se hur det kan hjälpa (eller stjälpa) en modell. Detta är ett standardverktyg i alla AI-olympiader.

Skapa fil: pca_digits.py.

Ladda och Visualisera:

import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
from sklearn.decomposition import PCA
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 1. Ladda data (bilder på siffror 0-9, 8x8 pixlar = 64 dimensioner)
digits = load_digits()
X, y = digits.data, digits.target

print(f"Original shape: {X.shape}") # (1797, 64)

# 2. Använd PCA för att krossa 64 dimensioner till 2
# Varje bild är 64 pixlar. Vi tvingar PCA att hitta de 2 "viktigaste" mönstren
# som bäst beskriver skillnaderna. Vi byter ut 64 pixel-värden mot 2 koordinater (x, y).
pca = PCA(n_components=2)
X_2d = pca.fit_transform(X)

# 3. Visualisera
plt.figure(figsize=(10, 8))
scatter = plt.scatter(X_2d[:, 0], X_2d[:, 1], c=y, cmap='jet', alpha=0.7)
plt.colorbar(scatter)
plt.title("Handskrivna siffror projicerade till 2D med PCA")
plt.show()

Analys: Ser du hur siffrorna klumpar ihop sig? Vilka siffror verkar lätta att blanda ihop?

Tävlingsmomentet: PCA som Feature Engineering Kör en Random Forest på originaldatan vs. PCA-datan.

# Dela upp data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)

# Modell 1: Original (64 features)
clf1 = RandomForestClassifier(n_estimators=50)
clf1.fit(X_train, y_train)
acc1 = accuracy_score(y_test, clf1.predict(X_test))

# Modell 2: PCA (använd t.ex. 10 komponenter istället för 2 för att behålla mer info)
pca_10 = PCA(n_components=10)
X_train_pca = pca_10.fit_transform(X_train)
X_test_pca = pca_10.transform(X_test) # OBS: Transformera testdatan med samma PCA!

clf2 = RandomForestClassifier(n_estimators=50)
clf2.fit(X_train_pca, y_train)
acc2 = accuracy_score(y_test, clf2.predict(X_test_pca))

print(f"Accuracy Original (64 dim): {acc1:.2%}")
print(f"Accuracy PCA (10 dim):      {acc2:.2%}")

Reflektion: Fick vi bättre eller sämre resultat med PCA? Gick det snabbare? I tävlingar handlar det ofta om att hitta balansen mellan att ta bort brus (bra för PCA) och att tappa information (dåligt för PCA).

https://www.nytimes.com/1958/07/13/archives/electronic-brain-teaches-itself.html ↩

Connectionism​

Neuronen​

Den artificiella neuronen​

En Neuron i Python​

Perceptronen​

Perceptronens lärande​

En Perceptron i Python​

1. Ritningen: __init__ metoden​

2. Gissningen: predict metoden (Steg 1)​

3. Lärandet: fit metoden (Steg 2 & 3)​

Steg 1: Test på vårt "fest-scenario"​

Steg 2: Perceptronen på ett riktigt dataset (Iris)​

Steg 3: Jämförelse med Scikit-learn​

Perceptronens svaghet​

Neurala Nätverk​

Variationer i input​

Variationer i output​

Backpropagation​

Träning av Neurala Nätverk​

Gradient Descent​

Backpropagation​

Ett Neuralt Nätverk i Python​

Byggstenen: En Passiv Neuron​

Tränaren: Nätverket​

Lös XOR – Ett Problem för ett Nätverk​

Träningskomponenterna: En Djupdykning​

1. Förlustfunktioner (Loss Functions)​

2. Optimerare (Optimizers)​

3. Aktiveringsfunktioner​

4. Att Stoppa Överträning (Regularization)​

5. Att tala nätverkets språk: One-Hot Encoding​

De Två Stora Familjerna av ML​

Supervised Learning (Övervakad Inlärning)​

Fallstudie 1: Linjär Regression​

Fallstudie 2: Beslutsträd i Praktiken​

Bortom Enskilda Träd: Ensemble-metoder​

Support Vector Machines (SVM) & The Kernel Trick​

Att Mäta Framgång: Bortom "Accuracy"​

Unsupervised Learning (Oövervakad Inlärning)​

1. Clustering (Klustring)​

2. Dimensionality Reduction (Dimensionsreducering)​

Dimensionsreduceringens Kung: PCA (Principal Component Analysis)​

Fallstudie: K-Means Clustering i Praktiken​

Fler Verktyg i Lådan​

Hantverket: Från Rådata till Modell​

1. Hantera det som saknas (NaNs)​

2. Feature Extraction & Engineering​

3. Skalning av data (Normalization)​

4. Validering: Cross-Validation​

5. Hyperparameter Tuning​

6. Tävlingstips: Hur man vinner en AI-olympiad​

Svenska exempel​

Perspektiv på Klassisk Maskininlärning​

Det filosofiska perspektivet: Empirismens Återkomst​

Det ekonomiska perspektivet: Från Akademisk Teori till Affärskritisk Motor​

Det sociologiska perspektivet: Filterbubblor och Polarisering​

Det kognitiva & psykologiska perspektivet: Uppmärksamhetsekonomin och den Algoritmiska Blicken​

Övningar​

Machine Learning

Övning 0: Bevisa Perceptronens Gränser​

Övning 1: Överlevare från Titanic​

Övning 2: Pingvin-hjärnan (multi-class & one-hot)​

Steg 1: One-Hot encoding av facit​

Steg 2: Bygg Pingvin-hjärnan​

Steg 3: Statistik​

Steg 4​

Steg 5: Hitta konflikter​

Övning 3: Uppgraderingen (Sigmoid)​

Övning 4: SimpleNeuralNetwork (Generalisering)​

Övning 5: Upp till bevis​

Övning 6: XOR med gömda lager​

Övning 7: XOR med gömda lager SOM LÄR SIG​

Övning 8: Ett generellt neuralt nätverk​

Övning 9: Modifiera ett Neuralt Nätverk​

Övning 10: "Hello World" för Neurala Nätverk (Siffror)​

Övning 11: Nya problem, samma kod​

Scenario A: Regression (Förutsäga Huspriser)​

Scenario B: Vin (Multi-class)​

Utforskaren: Dataset-menyn​

Övning 12: Kan ditt nätverk läsa?​

Connectionism

Neuronen

Den artificiella neuronen

En Neuron i Python

Perceptronen

Perceptronens lärande

En Perceptron i Python

1. Ritningen: `init` metoden

2. Gissningen: `predict` metoden (Steg 1)

3. Lärandet: `fit` metoden (Steg 2 & 3)

Steg 1: Test på vårt "fest-scenario"

Steg 2: Perceptronen på ett riktigt dataset (Iris)

Steg 3: Jämförelse med Scikit-learn

Perceptronens svaghet

Neurala Nätverk

Variationer i input

Variationer i output

Backpropagation

Träning av Neurala Nätverk

Gradient Descent

Backpropagation

Ett Neuralt Nätverk i Python

Byggstenen: En Passiv Neuron

Tränaren: Nätverket

Lös XOR – Ett Problem för ett Nätverk

Träningskomponenterna: En Djupdykning

1. Förlustfunktioner (Loss Functions)

2. Optimerare (Optimizers)

3. Aktiveringsfunktioner

4. Att Stoppa Överträning (Regularization)

5. Att tala nätverkets språk: One-Hot Encoding

De Två Stora Familjerna av ML

Supervised Learning (Övervakad Inlärning)

Fallstudie 1: Linjär Regression

Fallstudie 2: Beslutsträd i Praktiken

Bortom Enskilda Träd: Ensemble-metoder

Support Vector Machines (SVM) & The Kernel Trick

Att Mäta Framgång: Bortom "Accuracy"

Unsupervised Learning (Oövervakad Inlärning)

1. Clustering (Klustring)

2. Dimensionality Reduction (Dimensionsreducering)

Dimensionsreduceringens Kung: PCA (Principal Component Analysis)

Fallstudie: K-Means Clustering i Praktiken

Fler Verktyg i Lådan

Hantverket: Från Rådata till Modell

1. Hantera det som saknas (NaNs)

2. Feature Extraction & Engineering

3. Skalning av data (Normalization)

4. Validering: Cross-Validation

5. Hyperparameter Tuning

6. Tävlingstips: Hur man vinner en AI-olympiad

Svenska exempel

Perspektiv på Klassisk Maskininlärning

Det filosofiska perspektivet: Empirismens Återkomst

Det ekonomiska perspektivet: Från Akademisk Teori till Affärskritisk Motor

Det sociologiska perspektivet: Filterbubblor och Polarisering

Det kognitiva & psykologiska perspektivet: Uppmärksamhetsekonomin och den Algoritmiska Blicken

Övningar

Övning 0: Bevisa Perceptronens Gränser

Övning 1: Överlevare från Titanic

Övning 2: Pingvin-hjärnan (multi-class & one-hot)

Steg 1: One-Hot encoding av facit

Steg 2: Bygg Pingvin-hjärnan

Steg 3: Statistik

Steg 4

Steg 5: Hitta konflikter

Övning 3: Uppgraderingen (Sigmoid)

Övning 4: SimpleNeuralNetwork (Generalisering)

Övning 5: Upp till bevis

Övning 6: XOR med gömda lager

Övning 7: XOR med gömda lager SOM LÄR SIG

Övning 8: Ett generellt neuralt nätverk

Övning 9: Modifiera ett Neuralt Nätverk

Övning 10: "Hello World" för Neurala Nätverk (Siffror)

Övning 11: Nya problem, samma kod

Scenario A: Regression (Förutsäga Huspriser)

Scenario B: Vin (Multi-class)

Utforskaren: Dataset-menyn

Övning 12: Kan ditt nätverk läsa?

Analys: Vad hände precis?